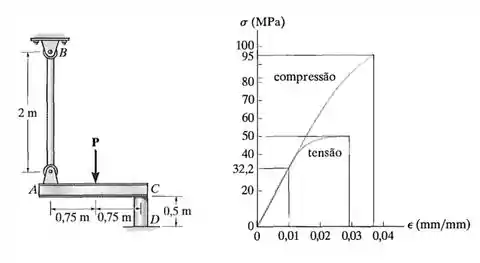
A figura apresenta o diagrama tensão-deformação para uma resina de poliéster. Se a viga for suportada por uma barra e um poste , ambos feitos desse material, e for submetida à carga , determine o ângulo de inclinação da viga quando a carga for aplicada. O diâmetro da barra é , e o diâmetro do poste é .
Passo 1
O que está acontecendo?
A barra e o poste estão contribuindo para o equilíbrio da viga através de forças e :

Aplicando as condições de equilíbrio para essa viga, conseguimos encontrar as forças e em função da carga .
Mas pelo princípio da ação e reação, se a barra e o poste fazem essas forças na viga, a viga var reagir com forças contrárias na barra e no poste:
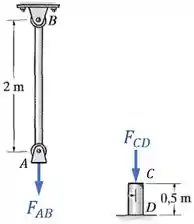
A força de tração na barra vai gerar nela uma força interna normal , enquanto que a força de compressão no poste vai gerar nele uma força interna normal .
Pessoal, se lembrem que a normal é negativa quando há compressão e positiva quando há tração.
Como uma consequência desse carregamento, a barra e o poste vão sofrer, respectivamente, variações de comprimento e , que vão poder ser calculadas através da fórmula
Sendo que:
- Os comprimentos dessas peças são , para a barra, e , para o poste;
- As duas peças vão ter o mesmo módulo de elasticidade , que pode ser encontrado a partir do Diagrama Tensão-Deformação fornecido;
- E as áreas das seções transversais dessas peças podem ser calculadas a partir de seus diâmetros, e , usando a fórmula .
E o que é que o exercício quer?
Ele quer que a gente descubra qual vai ser o ângulo de inclinação que a viga vai ganhar por causa das deformações/variações de comprimento na barra e no poste.
Agora, para analisar esse ângulo, vamos ter que encontrar primeiro as variações de comprimento e .
Então vamos começar o exercício determinando os valores do módulo de elasticidade e das forças normais na barra e no poste, para que depois a gente possa usar a fórmula .
Passo 2
Para encontrar o módulo de elasticidade do material, vamos recorrer a Lei de Hooke:
Isolando , temos que:
Então para calcular , precisamos de um par de valores para a tensão e a deformação que sigam a Lei de Hooke, o que é seguir a lei de Hooke? Isso significa que esses dois valores devem estar dentro na porção reta do diagrama (onde há deformação elástica).
Olhando para o Diagrama Tensão-Deformação do material, um par de valores desses já está marcado:
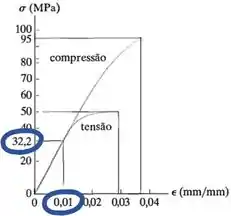
Usando esses valores, vamos ter que:
O que dá:
Ou, se preferirmos:
Passo 3
Já para encontrar as forças internas normais na barra e no poste, vamos primeiro fazer o diagrama de corpo livre da viga para encontrar as forças e em função da carga :
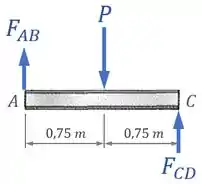
Aqui, podemos aplicar duas condições de equilíbrio: o equilíbrio de momentos e o equilíbrio de forças na vertical.
Pessoal, as forças e podem ser achadas por simetria e cada uma tem módulo igual à metade da força :
Por fim, como vimos no primeiro passo, temos que e que .
Dessa forma, encontramos que:
Passo 4
Agora que já encontramos o módulo de elasticidade e as forças normais , já temos todas as informações necessárias para calcular as variações de comprimento na barra e no poste. Visualizando esse efeito vamos ter:
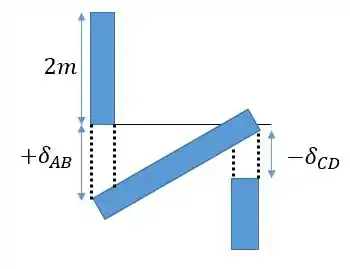
Aplicando a fórmula para a barra e para o poste , temos:
Podemos definir as áreas de seção transversal da barra e do poste a partir de seus diâmetros e usando a fórmula .
Além disso, temos que e .
Fazendo essas substituições, temos que:
Arrumando essas equações, elas ficam assim:
Agora só falta substituir os valores de e , além dos comprimentos e diâmetros da barra e do poste.
Fazendo essas substituições, temos:
Para as duas contas, temos que , de tal forma que as unidades “” e “” vão se cortar e o resultado final vai sair em .
Calculando tudo, encontramos:
Reescrevendo esses resultados em , temos:
Passo 5
Pronto, agora que já conhecemos as variação de comprimento na barra e no poste, só nos resta avaliar a nova inclinação da viga .
De um lado, temos que a barra vai se esticar , de tal forma que o ponto da viga vai descer essa distância.
Do outro, temos que o poste vai se comprimir , fazendo o ponto da viga descer essa distância.
Dessa forma, a disposição final da viga vai ficar assim:
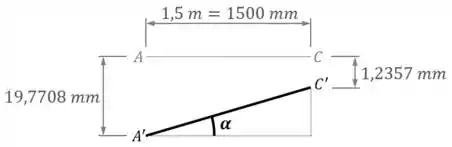
A tangente do ângulo de inclinação vai ser igual ao cateto oposto (igual à diferença entre e ) dividido pelo adjacente (igual ao comprimento de da viga):
O que dá:
Por fim, usando a função ou da nossa calculadora, encontramos nossa resposta: