Enunciado
Química - Fundamentos de química analítica, Skoog- Ed: 8º - Capítulo 7.Questões e Problemas - Ex. 27
Cinco laboratórios diferentes participaram de um estudo interlaboratorial envolvendo determinações dos níveis de em amostras de água. Os seguintes resultados são réplicas de determinações de de para os laboratórios A-E.
- Defina as hipóteses apropriadas.
- Os laboratórios diferem em um nível de confiança de 95%? E a um nível de confiança de 99% ()? E ao nível de confiança de 99,9% ()?
- Que laboratórios são diferentes dos outros em um nível de confiança de 95%?
Passo 1
Oi pessoal, vamos resolver esse exercício passo a passo, e tenho certeza que no final tirarei todas as suas dúvidas.
No item (a) queremos definir as hipóteses apropriadas, onde a hipótese nula () é quando duas ou mais quantidades observadas são iguais e a hipótese alternativa () é o complemento da hipótese nula, então para nosso exercício temos que:
Passo 2
No item (b) precisamos saber se existe diferença significativa entre os laboratórios, para isso iremos preencher o quadro abaixo passo a passo:
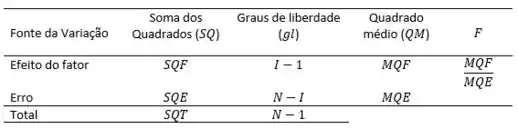
Como são cinco laboratórios:
E para cada laboratório temos 3 réplicas:
Com isso conseguimos definir nossos graus de liberdade. Para o fator:
Para o erro:
E do total:
Passo 3
Como queremos calcular a soma dos quadrados do fator () e do erro ():
Precisamos calcular a média e do desvio padrão de cada laboratório, para isso iremos utilizar as equações:
Então temos o seguinte:
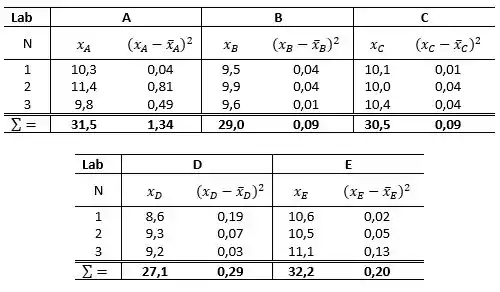
Com esses valores conseguimos calcular a média () e o desvio padrão ():
Agora conseguimos calcular a média global:
Por fim conseguimos calcular a Soma dos Quadrados do fator:
E do erro:
Agora podemos calcular os valores médios quadrados e :
E finalmente obtemos o valor é obtido a partir da seguinte equação:
Pela Tabela de distribuição , para 95% de confiança com 4 e 10 graus de liberdade, temos:
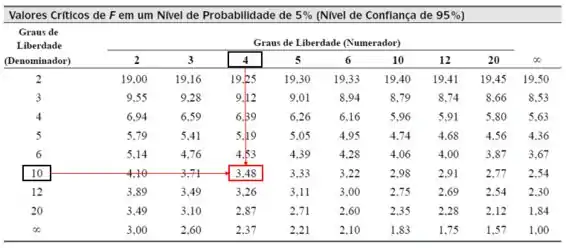
E pelo enunciado sabemos que para 99% de confiança, temos . E ao nível de confiança de 99,9%, .
Sendo assim, para o nível de confiança de 95% e 99% temos que , então há diferença entre os laboratórios. Porém, para 99,9% de confiança não há diferença, porque .
Passo 4
No item (c) queremos saber quais laboratórios diferem para um nível de confiança de 95%. Primeiro iremos organizar as médias em ordem crescente:
Foram realizadas 3 repetições para cada laboratório e iremos utilizar a equação da diferença menos significativa ():
Onde:
número igual de réplicas em cada grupo;
quadrado da média para o erro
com graus de liberdade relativo ao erro.
Pela Tabela da distribuição com 10 graus de liberdade e 95% de confiança:
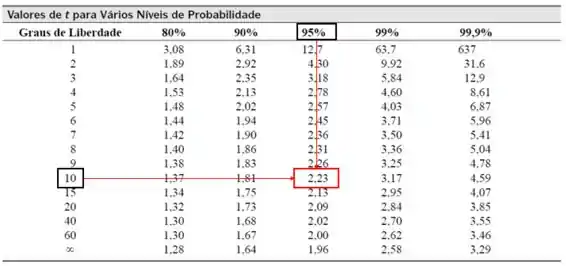
Logo:
Agora calculamos as diferenças nas médias e comparamos com 0,82. Para vários pares:
(menor);
;
;
;
(maior).
Testando cada par e comparando com 0,82:
(diferença significativa)
(diferença significativa)
(diferença significativa)
(diferença não significativa)
(diferença significativa)
(diferença significativa)
(diferença não significativa)
(diferença não significativa)
(diferença não significativa)
(diferença não significativa)
O laboratório D é diferente dos laboratórios A, C e E, mas não é diferente do laboratório B. O laboratório B difere dos laboratórios A e E, mas não difere do laboratório C. Não há diferença significativa entre os laboratórios A, C e E.
Até mais pessoal.
Resposta
- ;
- Os laboratórios diferem para um nível de confiança de 95% e 99%, mas não diferem no nível de confiança de 99,9%.
- O laboratório D é diferente dos laboratórios A, C e E, mas não é diferente do laboratório B. O laboratório B difere dos laboratórios A e E, mas não difere do laboratório C. Não há diferença significativa entre os laboratórios A, C e E.
.