Enunciado
Química - Fundamentos de química analítica, Skoog- Ed: 8º - Capítulo 7.Questões e Problemas - Ex. 22
A homogeneidade dos níveis de cloreto presente em uma amostra de água de um lago foi testada por meio de análises de porções retiradas do topo e do fundo da coluna de água, tendo apresentado os seguintes resultados, em de :
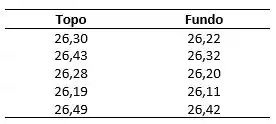
(a) Aplique o teste em um nível de confiança de 95% para determinar se as médias são diferentes.
(b) Agora use o teste pareado e determine se há diferença significativa entre os valores para o topo e fundo em um nível de confiança de 95%.
(c) Por que se chega a diferentes conclusões quando se usa o teste pareado e quando apenas se combina os dados e se usa o teste normal para diferenças nas médias?
Passo 1
Oi galerinha, vamos resolver esse exercício passo a passo. Vem comigo!
No item (a) queremos saber se há diferença entre as médias pelo teste . Para isso iremos, primeiramente, definir nossas hipóteses nula () e alternativa ():
O teste estatístico é determinado por:
Então primeiro iremos calcular a média para cada conjunto de dados ( e ), pela equação:
E o desvio padrão combinado (), pela equação:
Onde:
número total de conjunto de dados que estão sendo combinados.
Então:
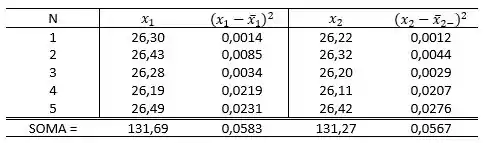
A média do topo:
E do fundo:
O desvio padrão combinado será:
Logo:
O número de graus de liberdade para encontrar o valor crítico de :
Então pela tabela, temos:
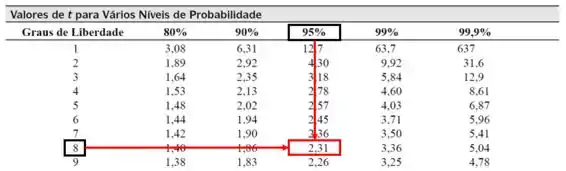
Como , aceitamos para um nível de confiança de 95% e concluímos que não há diferença entre as médias.
Passo 2
No item (b) queremos determinar se há diferença pelo teste pareado. Este é utilizado para cancelar a variação nas amostras e focalizar nas diferenças dos métodos. Se é a diferença média verdadeira entre os métodos, iremos testar as hipóteses:
O teste estatístico é:
Então primeiro iremos calcular a média e o desvio padrão da diferença ( e ), pelas equações:
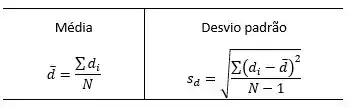
A diferença () entre os dados é dada por:
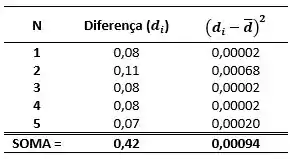
Sendo assim:
Agora conseguimos calcular o valor :
Com 95% de confiança e 4 graus de liberdade:
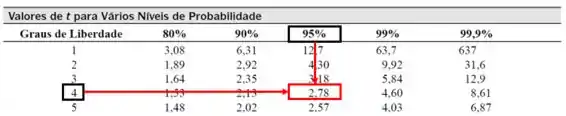
Como , rejeitamos para um nível de confiança de 95% e concluímos que há diferença entre as médias.
Passo 3
Se chega em diferentes conclusões, porque o nível de significância para o teste normal é apenas aproximado e o número de graus de liberdade é mais difícil de ser calculado, portanto, a grande variabilidade entre as médias mascara as diferenças entre o topo e o fundo da coluna de água. O pareamento dos dados permite que focalizamos nas diferenças.
Até mais pessoal.
Resposta
- Para um nível de confiança de 95% não há diferença entre as médias.
- Para um nível de confiança de 95% há diferença entre as médias.
- O nível de significância para p teste normal é apenas aproximado e o número de graus de liberdade é mais difícil de ser calculado, portanto, a grande variabilidade entre as médias mascara as diferenças entre o topo e o fundo da coluna de água. O pareamento dos dados permite que focalizamos nas diferenças.