Os dados na tabela que segue foram obtidos durante uma determinação colorimétrica de glicose em soro sangüíneo.
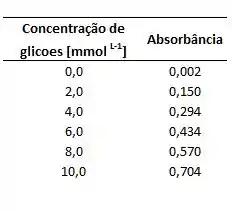
Faça a regressão linear, encontre a equação da reta pelo método dos mínimos quadrado e determine o coeficiente de correlação.
Passo 1
Para começar, vamos primeiro definir que a concentração de glicose será nosso e os valores de absorbância serão o nosso :

Para fazer a análise dos mínimos quadrados, também precisamos das médias de e , então vamos calculá-las:
Passo 2
Além das médias, também é importante calcular os quadrados e os quadrados das diferenças dos valores, assim como suas somas. Sendo assim, vamos expandir nossa tabela de apoio:
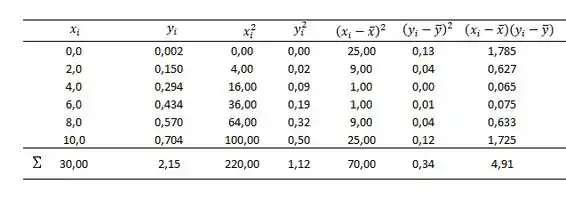
Com o auxílio dessa tabela podemos determinar:
E com isso, já conseguiresmo determinar os coeficientes da reta:
Como nossa reta é do tipo:
Ela será então:
Passo 3
Para calcular precisaremos de mais uma coluna na nossa tabela, a coluna de .
Como:
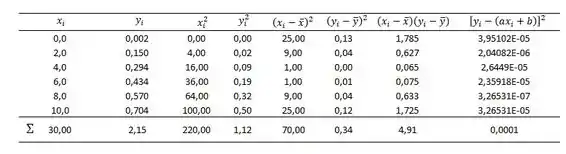
Logo:
O coeficiente de correlação pode ser calculado através da seguinte fórmula:
Onde:
Portanto: