Na determinação de um fármaco por fluorescência em meio ácido, foram obtidos os seguintes resultados:
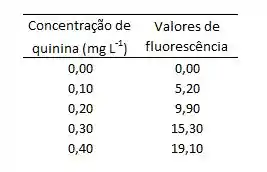
- Calcule o valor de e a equação da reta
- Considerando que a intensidade de uma amostra foi de , calcule o valor de quinina na amostra
- Calcule os desvio padrões e os intervalos de confiança a da inclinação e da interseção da reta.
Passo 1
Para começar, vamos primeiro definir que a concentração de quinina será nosso e os valores de fluorescência serão o nosso :
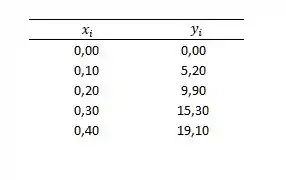
Para fazer a análise dos Mínimos quadrados, também precisamos das médias de e , então vamos calculá-las:
Passo 2
Além das médias, também é importante calcular os quadrados e os quadrados das diferenças dos valores, assim como suas somas. Sendo assim, vamos expandir nossa tabela de apoio:
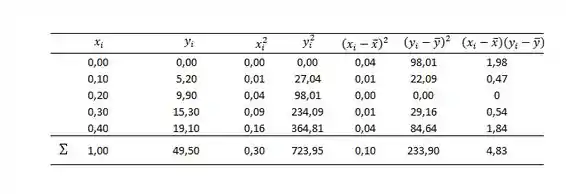
Com o auxílio dessa tabela podemos determinar:
E com isso, já conseguiresmo determinar os coeficientes da reta:
Como nossa reta é do tipo:
Ela será então:
Passo 3
Para calcular precisaremos de mais uma coluna na nossa tabela, a coluna de :

Como:
Logo:
O coeficiente de correlação pode ser calculado através da seguinte fórmula:
Onde:
Portanto:
Passo 4
Caso a intensidade de fluorescência em uma amostra fosse de , ou seja, nosso valor de , para achar a concentração da amostra, precisamos apenas aplicar esse valor na equação da reta encontrada, que foi:
Passo 5
Agora devemos calcular o desvio padrão e intervalo de confiança para a inclinação e a interseção. Para calular isso, primeiro precisamos calcular o desvio padrão da regressão () conforme a fórmula abaixo:
Com , pois é o número de pontos. Sendo assim, o desvio padrão da regressão será:
Para a inclinação, o desvio padrão será:
E o intervalo de confiança:
Onde é o coeficiente com grau de liberdade 2 graus menor que o número de pontos e nível de confiança de . Consultando uma tabela, teremos:
Portanto:
Para a interseção, a fórmula do desvio padrão é:
Usando os valores da tabela:
E o intervalo de confiança é calculado de maneira análoga: