Desenvolva uma análise de mínimos quadrados dos dados fornecidos pelas duas primeiras colunas da tabela abaixo que representa os dados obtidos na calibração para a determinação cromotográfica do isoctano em uma mistura de hidrocarbonetos
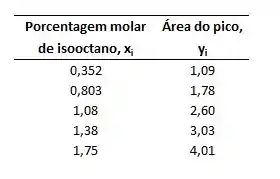
Passo 1
Bom pessoal, quando a questão pede para a gente fazer a análise do método dos mínimos quadrado, isso significa que a gente precisa fazer TUDO. Ou seja, calular a reta, o coeficiente de correlação, as variâncias e os intervalos de confiança.
Vamos começar então pelos médias:
Passo 2
Com os valores das médias, conseguiremos calcular tudo que precisamos na nossa tabela para então começar a fazer os nosso cálculos:
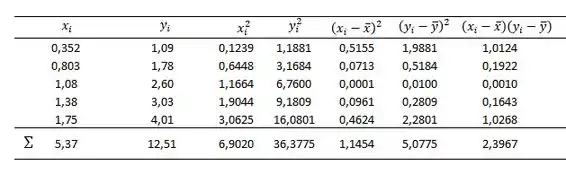
Com o auxílio dessa tabela podemos determinar:
E com isso, já conseguiresmo determinar os coeficientes da reta:
Como nossa reta é do tipo:
Ela será então:
Passo 3
Vamos partir agora para o cálculo nosso coeficiente de correlação, . Para isso, precisaremos de mais uma coluna na nossa tabela, a coluna de .
Como:
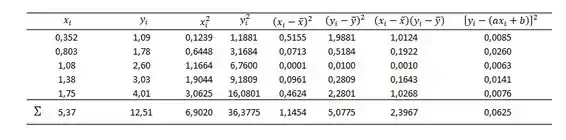
Logo:
O coeficiente de correlação pode ser calculado através da seguinte fórmula:
Onde:
Portanto:
Passo 4
Agora precisaremos calcular as variâncias e os intervalos de confiança do coeficiente angular e do coeficiente linear.
Porém, antes disso, precisaremos da variância da regressão, ela é dada por:
Substituindo os valores, teremos:
Passo 5
Vamos calular agora a variância do coeficiente angular (:
Substituindo tudo:
Com a variância de , podemos calcular seu intervalo de confiança, pela fórmula abaixo:
Onde é tem grau de liberdade duas unidades menor que oo número de pontos, ou seja, três. Como o enunciado não determinou o nível de confiança, vamos fazer para que é o nível de confiança mais usual. O valor de para grau de liberdade e nível de confiança é de . Portanto, nosso intervalo de confiança será:
Passo 6
Vamos fazer o mesmo agora para o coeficiente angular :
Substituindo na fórmula:
O intervalo de confiança será portanto: