Os dados na tabela a seguir representam o potencial de eletro verus a concentração .

- Transforme os dados em valores de versus
- Acha a equação da reta da regressãp linear de versus
- Encontre o coeficiente de correlação.
Passo 1
Primeiramente, devemos transformar nossos dados na coluna da concentração. Para obter uma relação linear entre os dois dados, precisaremos aplicar em todos os valores de concentração. Sendo assim, nossa nova tabela, será:
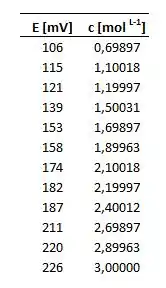
Passo 2
Agora, já poderemos começar a aplicar o método dos mínimos quadrados. Vamos chamar o potencial do eletro de e de .
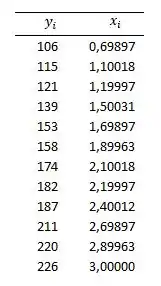
Podemos também calcular os valores de e :
Passo 3
Além das médias, também é importante calcular os quadrados e os quadrados das diferenças dos valores, assim como suas somas. Sendo assim, vamos expandir nossa tabela de apoio:

Com o auxílio dessa tabela podemos determinar:
E com isso, já conseguiresmo determinar os coeficientes da reta:
Como nossa reta é do tipo:
Ela será então:
Passo 4
Para calcular precisaremos de mais uma coluna na nossa tabela, a coluna de :
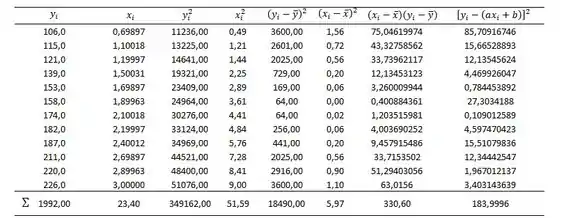
Como:
Logo:
O coeficiente de correlação pode ser calculado através da seguinte fórmula:
Onde:
Portanto: