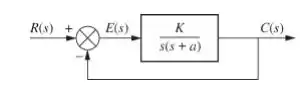
Dado o sistema da figura abaixo, calcule a sensibilidade da função de transferência em malha fechada a variaçãos no parâmetro . Como você poderia reduzir a sensibilidade?
Passo 1
Primeiramente vamos encontrar a nossa função de transferência. Por álgebra de diagrama de blocos teremos:
Sendo que é a função de transferência do processo, ou seja:
Passo 2
Para encontrar a sensibilidade da função de transferência em malha fechada em relação ao parâmetro , , devemos seguir a seguinte fórmula:
Ou seja, precisamos calcular a derivade de , em relação a . Como:
Passo 3
Substituindo na fórmula da sensibilidade:
Apesar da sensibilidade em relação ao parâmetro ser uma função de , dá pra ver que para qualquer valor de , um aumento no ganho vai diminuir a sensibilidade.
Resposta
É possível diminuir a sensisbilidade aumenta o ganho .