Determine a sensibilidade do erro em regime permanente a variações em e em para o sistema mostrado abaixo com uma entrada degrau.
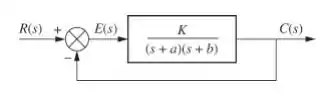
Passo 1
Primeiramente, vamos determinar o erro em regime permanente para esse sistema e entrada degrau:
Sendo assim, o erro em regime permanente pode ser calulado utilizando-se o teorema do valor final nessa fórmula:
Sendo que é a entrada, que nesse caso é um degrau e a função de transferência do processo que foi dada na figura aí em cima.
Portanto:
Passo 2
Sendo assim, a sensibilidade do erro em relação ao parâmetro será:
Usando a regra do quociente, podemos calcular:
Portanto:
Passo 3
Vamos fazer o mesmo agora para :
Usando a regra do produto novamente para calcular a derivada: