Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Sensibilidade

Ver Teoria
Exercício 21345678

Enunciado

Um sistema de malha fechada é usado para rastrear o sol e de modo a obter o máximo de energia a partir de um painel fotovoltaico. O sistema de rastreamento pode ser representado pela figura abaixo com:

H s = 1

G s = 100 τ s + 1

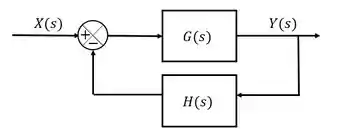
Com τ = 3 segundo, nominalmente. Determine a sensibilidade desse sistema para uma variação em τ .

Passo 1

Para calcular a sensibilidade do sistema em relação a τ , primeiramente precisaremos calcular a função de transferência do sistema. Vamos chamar essa função de T ( s ) e ela pode ser encontrada através de álgebra de diagrama de blocos conforme abaixo:

T s = Y s X s = G s 1 + G s H s = 100 τ s + 1 1 + 100 τ s + 1

Multipicando por τ s + 1 em cima e embaixo teremos:

T s = 100 τ s + 1 + 100 = 100 τ s + 101

Passo 2

Para encontrar a sensibilidade do sistema em relação a τ usaremos a fórmula para a sensibilidade que está aqui ó:

S τ T = ∂ T ∂ τ τ T

Precisamos, então, calcular essa derivada. Podemos fazer usando a expressão que encontramos acima e a regrinha do quociente que aprendemos em cálculo I há 84 anos atrás:

T s = 100 τ s + 101

∂ T ∂ τ = - 100 s τ s + 10 1 2

Passo 3

Substituindo a derivada e a expressão de T na fórmula da sensibilidade:

S τ T = - 100 s τ s + 1 01 2 τ 100 τ s + 101 = - 100 s τ s + 10 1 2 τ τ s + 101 10 0

Fazendo as simplificações, teremos:

S K e ∞ = - τ s τ s + 101

Como τ = 3 :

S τ T = - 3 s 3 s + 101

Resposta

S τ T = - 3 s 3 s + 101