Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Sensibilidade

Ver Teoria
Exercício 71234568

Enunciado

Um sistema digital de áudio é projetado para minimizar o efeito de perturbações e de ruído, como mostra a figura abaixo.

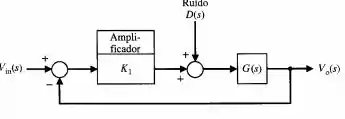
Como aproximação pode-se representar G s = K 2 . Calcule a sensibilidade do sistema com relação a K 2

Passo 1

Primeiramente, vamos usar álgebra de diagrama de blocos para calcular a função de transferência do sistema em malha fechada.

T s = V 0 s V i n s = G s K 1 + D s 1 + K 1 G ( s )

Como G s = K 2 teremos:

T s = K 2 K 1 + D s 1 + K 1 K 2

Passo 2

Vamos usar a fórmula da sensibilidade para conseguir determinar a sensibilidade do sistema em relação a K 2

S K 2 T = ∂ T ∂ K 2 K 2 T

Primeiramente, vamos calcular essa derivada enjoada aí. Como:

T s = K 2 K 1 + D s 1 + K 1 K 2

Podemos usar a regra do quociente e encontrar

∂ T ∂ K 2 = K 1 + D s 1 + K 1 K 2 - K 1 K 2 K 1 + D s 1 + K 1 K 2 2

Passo 3

Substituindo tudo na expressão da sensibilidade teremos:

S K 2 T = ∂ T ∂ K 2 K 2 T = K 1 + D s 1 + K 1 K 2 - K 1 K 2 K 1 + D s 1 + K 1 K 2 2 K 2 K 2 K 1 + D s 1 + K 1 K 2

Fazendo as simplificações, teremos:

S K 2 T = 1 + K 1 K 2 - K 1 K 2 1 + K 1 K 2 = 1 1 + K 1 K 2

Resposta

S K 2 T = 1 1 + K 1 K 2