Determine a sensibilidade do erro em regime permanente para uma entrada rampa do sistema abaixo em relação a e .
Passo 1
Antes de mais nada, precisamos definir a nossa fórmula do erro em regime permanente.
O erro pode ser calculado como:
Sendo assim, o erro em regime permanente pode ser calulado utilizando-se o teorema do valor final nessa fórmula:
Sendo que é a entrada e a função de transferência do processo.
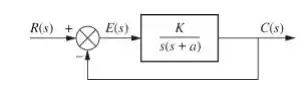
Para o nosso exercício, temos uma entrada rampa e a função de transferência é dada na figura:
Portanto:
Passo 2
Sendo assim, a sensibilidade do erro em relação ao parâmetro será:
Como:
Teremos:
Passo 3
E a sensibilidade em ralação ao ganho será:
Como:
Esses resultados indicam que não é possível aumentar ou diminuir a sensibilidade do erro em regime permanente em relação a esses parâmetros. O sinal negativo na sensibilidade do ganho acontece porque um aumento em causa uma diminuição de , e vice-versa.