Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Sensibilidade

Ver Teoria
Exercício 51234678

Enunciado

Um sistema de controle é representado pelo diagrama de blocos abaixo:

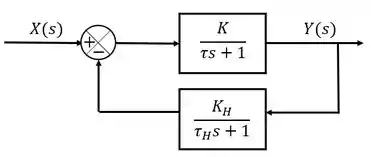
Encontre a sensisbilidade desse sistema com relação à constante de tempo do transmissor, τ H .

Passo 1

Vamos começar determinando a função de transferência em malha fechada do sistema.

Usando as regrinhas de álgebra de diagrama de blocos teremos:

T s = Y s X s = K τ s + 1 1 + K τ s + 1 K H τ H s + 1

Rerranjando essa função de transferência teremos:

T s = K τ s + 1 ( τ H s + 1 ) ( τ s + 1 ) + K K H τ H s + 1 = K τ H s + 1 [ ( τ H s + 1 ) ( τ s + 1 ) + K K H ] τ s + 1

Passo 2

Para calcular a sensibilidade, vamos aplicar a fórmula abaixo:

S τ H T = ∂ T ∂ τ H τ H T

Vamos começar, calculando a derivada ∂ T ∂ τ H . Como:

T s = K τ H s + 1 [ ( τ H s + 1 ) ( τ s + 1 ) + K K H ] τ s + 1

Podemos usar a regra do quociente e encontrar ∂ T ∂ τ H :

∂ T ∂ τ H = K s [ ( τ H s + 1 ) ( τ s + 1 ) + K K H ] τ s + 1 - K s ( τ s + 1 ) ² τ H s + 1 { [ ( τ H s + 1 ) ( τ s + 1 ) + K K H ] τ s + 1 } ²

Passo 3

Substituindo tudo na expressão da sensibilidade teremos:

S τ H T = ∂ T ∂ τ H τ H T = K s [ ( τ H s + 1 ) ( τ s + 1 ) + K K H ] τ s + 1 - K s ( τ s + 1 ) ² τ H s + 1 { [ ( τ H s + 1 ) ( τ s + 1 ) + K K H ] τ s + 1 } ² τ H K τ H s + 1 [ ( τ H s + 1 ) ( τ s + 1 ) + K K H ] τ s + 1

Meu deus, ficou enorme! Mas calma que dá pra simplificar um pouco:

S τ H T = s [ ( τ H s + 1 ) ( τ s + 1 ) + K K H ] - K s ( τ s + 1 ) τ H s + 1 [ ( τ H s + 1 ) ( τ s + 1 ) + K K H ] τ H τ H s + 1

Resposta

S τ H T = s [ ( τ H s + 1 ) ( τ s + 1 ) + K K H ] - K s ( τ s + 1 ) τ H s + 1 [ ( τ H s + 1 ) ( τ s + 1 ) + K K H ] τ H τ H s + 1