Encontre , usando série de Taylor gerada por em , sabendo que:
Passo 1
Lembrando que a série de Taylor é definida por:
Como todos os valores das derivadas da função estão em torno de , vamos fazer a série com . Em torno de temos:
O que temos que fazer agora é substituir os valores da tabela e achar o polinômio correspondente.
Passo 2
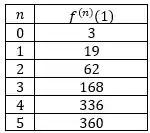
A tabela é:
Por essa tabela conseguimos montar o polinômio aplicando os valores na fórmula de Taylor:
Prontinho!! Esse é o nosso polinômio!