Obtenha as aproximações linear e quadrática para , em torno de usando a fórmula de Taylor.
Em um mesmo gráfico, esboce a curva e as aproximações linear e quadrática obtidas em . Através do gráfico analise o comportamento das aproximações constando que representam apenas localmente. Qual das duas curvas você escolheria para aproximar em torno de .
Obs.: Os gráficos podem ser esboçados a mão ou traçados usando software ou ainda na calculadora.
Passo 1
Nessa letra ele quer simplesmente os polinômios de Taylor de graus e . Temos:
, :
, :
Passo 2
O próximo passo é esboçar o gráfico disso. Fica assim oh:
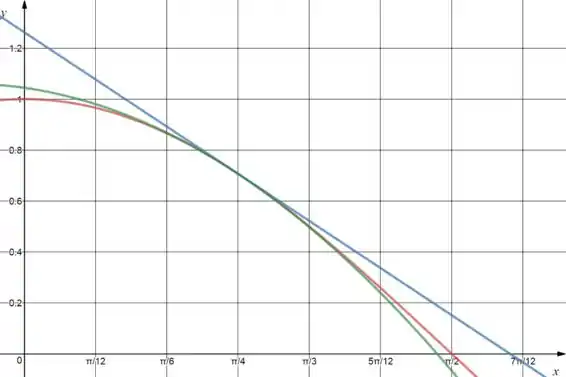
Como era de se esperar todas as aproximações têm o valor exato em . A curva azul é o polinômio de Taylor de grau e a curva vermelha é o polinômio de Taylor de grau .
Outra conclusão que chegamos por meio desse gráfico é que em torno de , o polinômio de Taylor de grau é uma aproximação melhor que o de grau .
Resposta
:
:
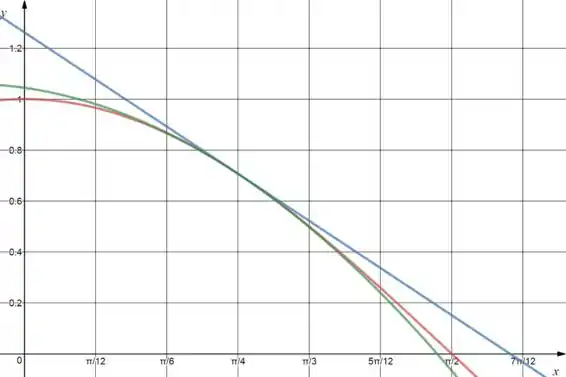
Todas as aproximações têm o valor exato em . Em torno de , o polinômio de Taylor de grau é uma aproximação melhor que o de grau .