Para a malha de controle abaixo, obtenha as fórmulas de sintonização para um PID real utilizando o método de síntese direta. Considere:
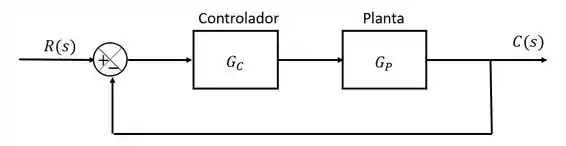
A resposta do sistema desejada é a resposta de primeira ordem sem tempo morto.
Passo 1
A função de transferência para o sistema do enunciado é:
Manipulando essa expressão para obter uma fórmula de síntese ara teremos::
Como desejamos uma resposta de primeira ordem sem tempo morto, podemos fazer a seguinte substituição:
Onde é a constante de tempo da resposta:
Fazendo a substituição, teremos:
Rearranjando:
Passo 2
A função de transferência do processo, dada no enunciado foi a seguinte:
Substituindo na fórmula do controlador, teremos:
Rearranjando um pouco:
Podemos comparar essa fórmula com a fórmula de um PID em série:
O controlador PID em série, diferentemente do PID convencional, apresenta os blocos proporcional, integral e derivativo em série, fazendo com que essas parecelas se multipliquem na função de transferência ao invés de se somar.
Passo 3
Por fim, precisamos apenas comparar as duas expressões e encontrar as fórmulas para os parâmetros do controlador.
Como o controladore encontrado é um PID, precisamos definir os três parâmetros desse controlador, , e . Por comparação, podemos encontrar as correalações: