A saída de uma caixa registradora o custo total de itens registrados pelo caixa. A entrada é o custo do n-ésimo item:
(a) Escreva a equação relacionando com a entrada .
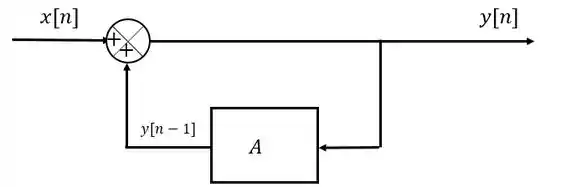
(b) Represente o diagrama de blocos desse sistema usando um elemento de atraso de tempo.
Passo 1
A saída representa a soma de todos os itens vendidos até aquele momento. Cada item tem valor , sendo assim, podemos escrever como:
A expressão acima está correta e poderia ser a resposta, entretanto existe uma forma mais elegante de escrever isso (e também vai ajudar a gente pro item b)
Analogamente à forma como escrevemos a expressão de , podemos também escrever a expressão de :
Podemos ver que a é igual à toda a parte final da expressão de , podemos então fazer a substituição e ficaremos com:
Passo 2
O diagrama de blocos para o sistema poderá ser representado da seguinte maneira:
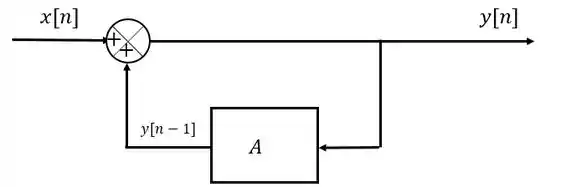
Para gerar a saída devemos somar a entrada com a própria saída atrasada . Sendo assim, a gente realimenta o sistema com a própria saída, mas antes de somá-la à entrada, ela deve passar por um bloco de onde ela sairá atrasada.
Resposta