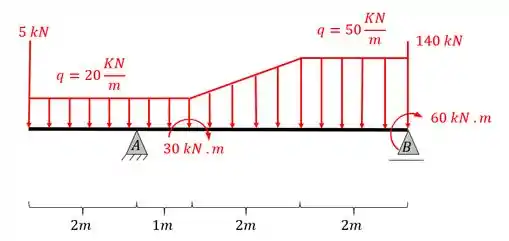
Calcule as reações de apoio da viga dada abaixo.
Passo 1
Já vimos que para solucionar a nossa viga precisamos seguir uma sequência de passos que vai nos ajudar a achar a equações de cada trecho, para isso devemos fazer o seguinte
- Primeiro definimos quais serão os trechos com equações, que definimos como sendo o ponto em que há mudança brusca de carregamento
- Depois usamos as equações de equilíbrio para determinar as reações de apoio.
- Em seguida definimos uma equação para nossa carga distribuída ou concentrada
- Por fim usamos as seguintes fórmulas, com suas condições de contorno para encontrarmos as equações de cortante e momento fletor
- Não é o caso do nosso problema, mas ainda pode ter o último passo que é o desenho dos diagramas, porém, iremos apenas até o passo anterior com a definição das equações.
Dito tudo isso, vamos pôr a mão na massa!!!
Passo 2
Como vimos, o objetivo da nossa questão são apenas as reações de apoio, por isso, iremos até o passo 2 que vimos acima. Um macete legal é trocarmos todas as cargas distribuídas que tivermos no nosso enunciado por cargas concentradas, no nosso caso temos apenas uma carga do tipo retangular, e nesse caso teremos que o nosso vetor concentrado que representa o distribuído será
Assim
O trapezoidal vamos dividir em duas regiões
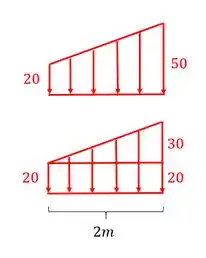
A parte retangular inferior será
A parte triangular será
E no triangular a distancia do lado zero do triangulo será 2/3 do vão
Dessa forma o nosso carregamento ficará da seguinte maneira na estrutura
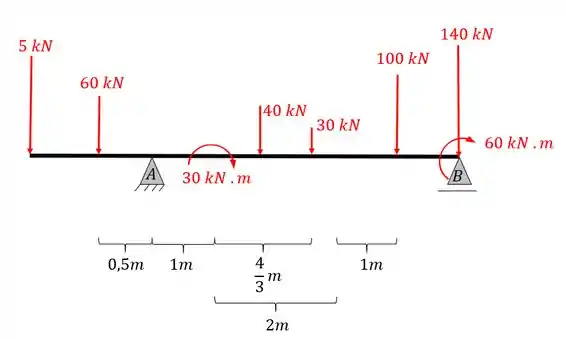
Passo 3
Agora que já determinamos os trechos e a equação, vamos determinar as reações de apoio, já que na nossa listinha esse é o passo 2, usando as equações de equilíbrio e definindo o diagrama de corpo livre, teremos
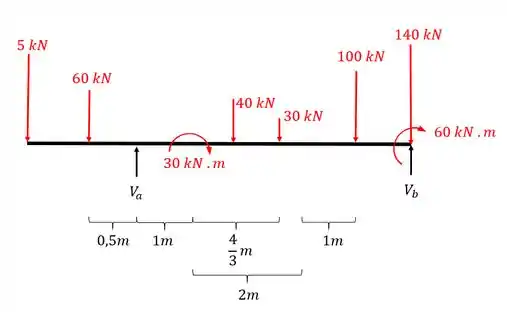
Perceba que trocamos os apoios por reações de apoio