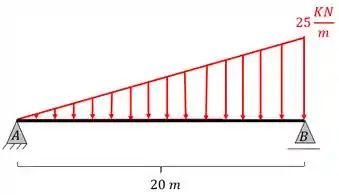
Determine as equações de cortante e momento fletor da viga simples dada abaixo, com carregamento triangular. Não se esqueça de analisar as características pertinentes a carregamentos triangulares.
Passo 1
Já vimos que para solucionar a nossa viga precisamos seguir uma sequência de passos que vai nos ajudar a achar a equações de cada trecho, para isso devemos fazer o seguinte
- Primeiro definimos quais serão os trechos com equações, que definimos como sendo o ponto em que há mudança brusca de carregamento
- Depois usamos as equações de equilíbrio para determinar as reações de apoio.
- Em seguida definimos uma equação para nossa carga distribuída ou concentrada
- Por fim usamos as seguintes fórmulas, com suas condições de contorno para encontrarmos as equações de cortante e momento fletor
- Não é o caso do nosso problema, mas ainda pode ter o último passo que é o desenho dos diagramas, porém, iremos apenas até o passo anterior com a definição das equações.
Dito tudo isso, vamos pôr a mão na massa!!!
Passo 2
Já temos um trecho, que nesse caso é o trecho AB. Podemos observar que dentro do trecho AB não há sub trechos, já que estamos apenas no trecho triangular e não há nem apoio e nem cargas concentradas nesse trecho, com isso já executamos a primeira parte do nosso passo a passo.
Antes de determinamos as reações de apoio vamos montar uma equação que compatibilize com o carregamento do trecho AB, dessa forma, imagine que colocamos o nosso triângulo em um plano cartesiano.
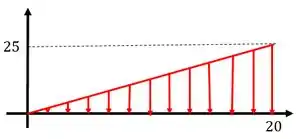
Agora é só determinar a equação da reta, usando a equação
Substituindo os nossos dados teremos
Resolvendo o sistema teremos
Logo a nossa equação será
Passo 3
Agora que já determinamos os trechos e a equação, vamos determinar as reações de apoio, já que na nossa listinha esse é o passo 2, usando as equações de equilíbrio e definindo o diagrama de corpo livre, teremos
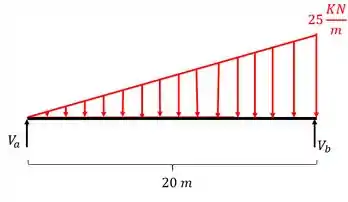
Vale relembrar que em carregamentos triangulares a resultante fica a 2/3 da base com relação ao menor lado ou a 1/3 da base em relação ao maior lado, é muito importante lembrar disso na hora de fazer a conta, pois irá influenciar no cálculo do momento fletor.
- Trecho AB
- X=0
- X=0
E assim terminamos o nosso segundo passo
Passo 4
Já sabemos a equação do nosso carregamento, definimos ele no nosso passo 2, mas para integração precisamos tomar muito cuidado, porque precisamos trocar o sinal do nosso carregamento, dessa forma, teremos que
Não se esqueça que sempre definimos a nossa carga com o sinal contrário para podermos fazer a integração.
Com isso já podemos ira pra o passo de determinação das equações, fazendo para cada trecho teremos,
Perceba que pelas condições de contorno que quando estamos exatamente em cima do nosso ponto A, logo o nosso cortante nesse ponto é a própria reação de apoio em A. que nesse caso está para cima, e sempre que fizemos uma análise vindo pela esquerda com o vetor para cima ele será positivo.
Substituindo na nossa equação teremos
Com isso a nossa equação do cortante será
Para calcular o momento fletor teremos que usar a outra fórmula, com isso teremos
Perceba que pelas condições de contorno que quando estamos exatamente em cima do nosso apoio A, logo o nosso momento fletor nesse ponto é zero, já que nosso apoio é do segundo gênero, e definiremos como positivo todos os momentos que tracionarem as fibras da parte de baixo, e negativo todos os vetores que estiverem tracionando as fibras da parte de cima,
Substituindo na nossa equação teremos
Com isso a nossa equação do momento fletor será
Com isso atendemos os pedidos do nosso enunciado, descobrindo as equações do trecho AB assim como as extremidades desse trecho. Agora é só ficar tranquilo pra poder integrar os trechos que forem necessários e treinar mais um pouco, beleza, vamos aos exercícios então.
Resposta
Equações trecho AB
Cortante
Momento fletor