(Adaptado) Um chip, com base quadrada de lado e espessura , é montado em um substrato. O substrato comporta-se como um isolante ideal. O chip é resfriado por convecção forçada de ar através da sua superfície superior, que é a única não isolada pelo substrato.
A temperatura do ar é e o coeficiente de transferência de calor é . O chip encontra-se inicialmente desligado e em equilíbrio com o ar. Quando o chip é ligado, energia é gerada uniformemente em seu interior com uma taxa volumétrica .
Forneça:
Formulação matemática do problema.
Solução analítica.
Passo 1
Formulação matemática do problema.
Para chegar à formulação matemática, vamos partir da equação de calor, dada por:
Vamos fazer as seguintes considerações:
- Condução de calor unidimensional;
- Condução transiente;
- Propriedades constantes;
Assim, a equação de calor pode ser escrita da seguinte forma:
![]()
Para condição inicial, o problema nos disse que o chip encontra-se inicialmente em equilíbrio com o ar, assim:
![]()
Como condições de contorno, o problema nos disse que uma das superfícies está termicamente isolada , e há troca de calor por convecção com o ar na outra superfície .
Assim:
![]()
![]()
Passo 2
Solução analítica.
Nós vamos dividir a solução em uma solução homogênea (que vamos calcular a partir das soluções tabeladas) e uma solução particular (não-homogênea, que teremos que resolver), que depende somente de .
Assim:
Aplicando isso à nossa formulação matemática, teremos:
Separando os dois problemas, teremos:
Passo 3
Começando pela solução homogênea:
Pelas condições de contorno, este corresponde ao caso 6 da nossa tabela, onde:
Sendo as raízes da seguinte expressão:
Sendo . Assim, a solução homogênea será dada por:
Agora é arrumar a casa:
Vamos resolver essa integral separadamente:
Finalmente, a solução homogênea será:
Onde é a raiz de:
A partir da expressão acima, podemos chegar à expressão de da seguinte forma:
A partir dessa expressão da tangente, podemos pensar no seguinte triângulo retângulo:
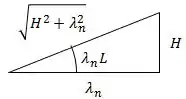
Onde:
Finalmente:
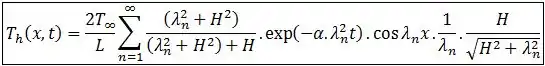
Passo 4
Para a solução particular, temos que:
Integrando uma vez a equação duas vezes, temos que:
Aplicando à primeira condição de contorno, para :
Assim:
Aplicando a segunda condição de contorno, para :
Substituindo a expressão de que acabamos de encontrar:
![]()
Passo 5
Finalmente, a solução analítica do problema será:
Substituindo as soluções:
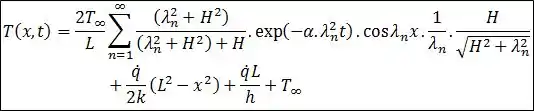
Resposta