Uma placa de aço , com espessura , encontra-se inicialmente na temperatura uniforme . As duas superfícies da placa são então mantida na temperatura . Para este problema, considerando propriedades físicas constantes, forneça:
Formulação matemática;
Solução analítica;
Temperatura do centro da placa 10 minutos depois de iniciado o resfriamento.
Passo 1
Formulação matemática.
Para chegar à formulação matemática, vamos partir da equação de calor, dada por:
Vamos fazer as seguintes considerações:
- Condução de calor unidimensional;
- Condução transiente;
- Propriedades constantes;
- Não há geração térmica.
Assim, a equação de calor pode ser escrita da seguinte forma:
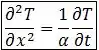
Para condição inicial, o problema nos disse que:
![]()
Como condições de contorno, o problema nos disse que as superfícies são mantidas a . Assim:
![]()
![]()
Passo 2
Solução analítica;
Nesse caso, como as temperaturas em ambos os lados da placa são iguais, podemos transformar esse problema em homogêneo utilizando , tal que:
Fazendo isso, a formulação matemática passa a ser dada por:
Pelas condições de contorno, este corresponde ao caso 1 da nossa tabela, onde:
Sendo as raízes da seguinte expressão:
Assim, a solução homogênea será dada por:
Agora é arrumar a casa:
Vamos resolver essa integral separadamente:
Finalmente, a solução homogênea será:
Onde é a raiz de:
O seno é nulo para qualquer múltiplo de . Assim:
Dessa forma, substituindo na expressão da solução homogênea:
Repare que, para valores pares de , e, para valores ímpares, . Assim, podemos levar somente em consideração os valores ímpares de , substituindo o na equação por . Dessa forma:
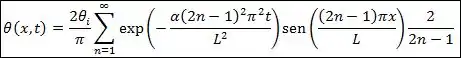
Substituindo de volta a temperatura :
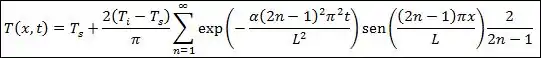
Passo 3
Temperatura do centro da placa 10 minutos depois de iniciado o resfriamento.
Como queremos a temperatura no centro da placa, vamos considerar . Assim, substituindo os valores, onde:
Considerando apenas o primeiro termo da série , teremos:
Jogando isso tudo na calculadora:
![]()
Resposta