Determine se a água é um vapor superaquecido, um líquido comprimido ou se ela está saturada, usando a tabela de propriedades dada. Além disso, determine se a água está na região de saturação, na região de vapor superaquecido ou na região de líquido comprimido, localizando o seu estado na superfície termodinâmica. Considere que a temperatura da água seja de e a sua pressão seja .
Passo 1
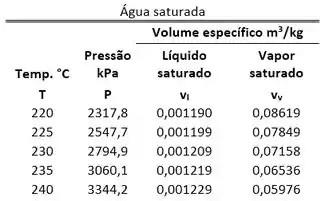
Para saber se a água está em uma dessas três opções, devemos comparar sua pressão com a pressão de saturação.
Caso ela tenha pressão menor que a pressão de saturação, ela é um vapor superaquecido!
Caso ela tenha pressão igual à pressão de saturação, ela estará saturada.
Caso ela tenha pressão maior que a pressão de saturação, ela é um líquido comprimido!
O enunciado informa que:
Então agora vamos comparar esses valores com as condições de saturação da água informadas pela tabela! Mas não podemos fazer isso agora! A tabela do enunciado informa as pressões de saturação para diversos valores de temperatura. O problema é que nenhum desses valores de temperatura é igual ao valor de temperatura da água! Resolveremos isso no próximo passo!
Passo 2
Achamos o valor de pressão de saturação para a temperatura certa, calculando seu valo através da interpolação! E como fazemos isso? Considerando que a pressão de saturação saturado varia linearmente com a temperatura para temperaturas intermediárias que não existem na tabela. Ou seja:
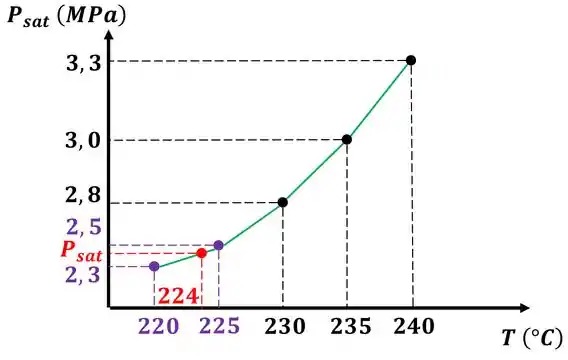
Determinamos uma pressão que está no meio de outros dois valores de pressão informados pela tabela, calculando a equação da reta que liga a menor temperatura do intervalo com a maior temperatura do intervalo .
No caso estudado, a temperatura da água vale . Por causa disso, ela está no meio do intervalo entre a temperatura menor de e a temperatura maior de .
Sabendo disso, precisamos encontrar a equação da reta que liga esses dois pontos!
Fica faltando saber qual é a região que o estado da água está. Descobrimos isso, olhando para a superfície termodinâmica.
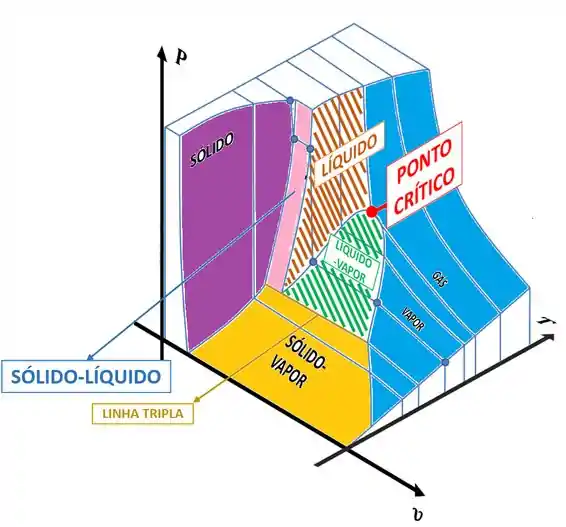
Cada região tem uma cor. Se a água for vapor superaquecido, o estado dela estará dentro da região azul. Se a água for líquido comprimido, o estado dela estará dentro da região vermelha. E se a água estiver saturada, o estado dela estará dentro da região verde!
Agora vamos aprender a interpolar!
Passo 3
A equação da reta tem duas formas:
Ou:
Visualizamos essa informação através da imagem abaixo:
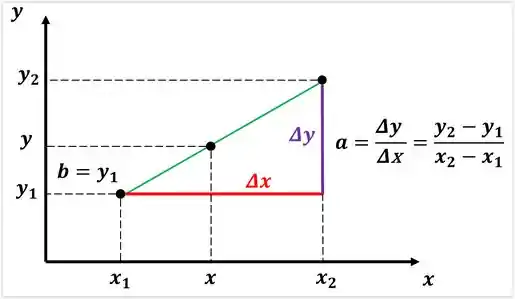
Para o nosso caso a variável é a nossa tempertura e a variável dependente é a pressão de saturação, porque é sempre o valor da propriedade que queremos interpolar. Logo:
é o valor da temperatura para a qual queremos encontrar a pressão de saturação.
é o valor inferior do intervalo. Ele é o valor inferior de temperatura do intervalo.
é o valor superior do intervalo. Ele é o valor superior de temperatura do intervalo.
é o valor interpolado da pressão de saturação.
é o valor da propriedade que queremos encontrar relativo ao valor inferior de temperatura. Ele é o valor da pressão de saturação para a temperatura inferior.
é o valor da propriedade que queremos encontrar relativo ao valor superior de temperatura. Ele é o valor da pressão de saturação para a temperatura superior.
No próximo passo substituiremos todos esses valores na fórmula da reta.
Passo 4
Pronto, achamos o valor interpolado de pressão de saturação! Na próxima etapa, a gente vai comparar esse valor com a pressão da água informada pelo enunciado.
Passo 5
Vemos que para a pressão de saturação da água vale . Ou seja:
Comparando a pressão da água com a sua pressão de saturação, vemos que:
Logo a água é um vapor superaquecido. Por causa disso, o estado da água está em algum ponto da região azul da superfície termodinâmica.
Resposta
A água é um vapor superaquecido e está na região azul da superfície termodinâmica.