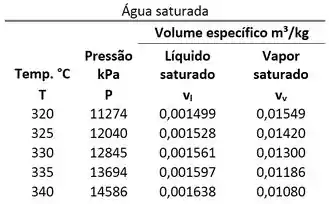
Qual é o volume específico da mistura saturada de água líquida com vapor d’água a com um título de ? Use a tabela de propriedades abaixo.
Passo 1
O enunciado pede que a gente calcule o volume específico médio da mistura bifásica . Precisamos descobrir esse valor através das duas propriedades dadas:
é o título da água. Ou seja, é a porcentagem de massa da mistura que é vapor.
é a temperatura da mistura.
A fórmula de volume específico médio em função do título é:
onde:
- é o volume específico do líquido saturado presente na mistura. Seu valor depende da temperatura . Descobrimos seu valor através da tabela;
- é o volume específico do vapor saturado presente na mistura. Seu valor depende da temperatura . Descobrimos seu valor através da tabela;
Falta saber quanto valem os volumes específicos das fases saturadas, mas a tabela não tem esses valores para a temperatura de . Ou seja, precisamos interpolar essas duas propriedades para descobrí-los. Entenderemos isso na próxima etapa!
Passo 2
Para interpolar, vamos considerar que os volumes específicos saturados variam linearmente entre uma temperatura da tabela e outra temperatura vizinha da tabela. Por causa dessa aproximação, os volumes específicos serão obtidos a partir da equação da reta que passa pelos dois pontos mais próximos de . No ponto 1 da reta, a temperatura é:
Além disso, seus volumes específicos saturados são:
No ponto 2 da reta, temos:
Além disso, seus volumes específicos saturados são:
Como uma reta é definida por dois pontos diferentes, a equação das duas retas que calculam os volumes específicos já está definida:
Substituindo os valores mostrados de , , , , , e nas fórmulas, achamos os volumes específicos finais. Com essas propriedades, achamos o volume específico médio pela fórmula dele. Então vamos começar a substituir os dados! É isso que faremos na próxima etapa!
Passo 3
Começando pelo volume específico do líquido saturado:
Para o volume específico do vapor saturado, temos:
Agora usaremos esses resultados na expressão de volume específico médio para chegar na resposta final.
Tá vendo? O que é bom acaba rápido! Já terminamos o exercício! ;-)