Para o campo de tensão bidimensional da Figura abaixo considere que
Calcule:
a tensão de cisalhamento
a tensão de cisalhamento no plano .
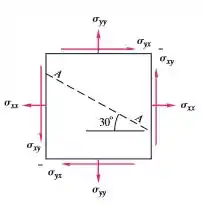
Passo 1
Como vimos na questão anterior, quando fazemos o corte temos a seguinte configuração:
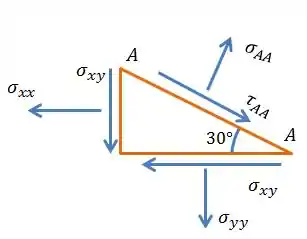
O equacionamento será feito igualzinho fizemos no exercício anterior, decompondo as tensões na direção do corte.
Repara que igualamos , porque o elemento não está sujeito à rotação.
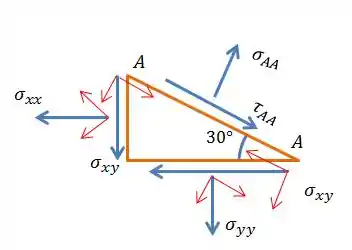
E na hora de equacionar, temos que lembrar que a lei de Newton é “somatório de forças igual a zero”, e o que temos é tensão. Pra transformar a nossa tensão em força, devemos multiplicá-la por uma área. Então consideramos a “profundidade” do elemento constante e multiplicamos as tensões pelo comprimento da “aresta” no qual cada tensão está atuando. Vamos definir o comprimento do corte como , então:
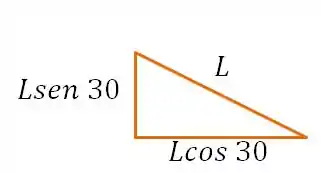
Agora vamos por todas as pressões na direção normal ao corte, multiplicando elas pelo comprimento do respectivo lado, beleza?
E assim vamos obter a seguinte equação:
Isso, nada mudou até agora em relação ao exercício anterior. O que vai mudar vai ser agora: não temos mais o valor de , mas temos o valor de .
Assim, cortando e substituindo os valores que temos, chegamos em:
Repare que todas as unidades são múltiplas de 1000. Então podemos escrever todas elas divididas por 1000 e vamos encontrar o resultado em .
Podemos isolar :
E resolvendo a equação, encontramos o valor de :
Passo 2
Bem, agora que temos a tensão , podemos igual fizemos na questão anterior resolver o problema.
Basta equacionarmos todas as pressões que atuam na direção de cisalhamento .
Cortando o e substituindo os valores dado no enunciado para descobrir temos: