Calcule para o campo onde é a curva orientada no sentido positivo e composta por
Passo 1
Vamos lá, galera!
Essa curva é composta por vários pedaços, vamos juntar tudo em um esboço pra ver como fica
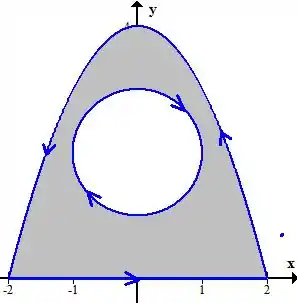
Aparentemente aqui podemos usar o Teorema de Green, né? O teorema é esse aqui, onde é a fronteira da região .
No nosso caso, a região é aquela sombreada ali no esboço. Precisamos primeiro encontrar esse termo e delimitar a região , depois é só integrar.
Passo 2
Vamos começar calculando
Derivando em relação a , temos:
Derivando em relação a , temos:
Substituindo lá em cima
Opa os termos esquisitos se cortaram:
Voltando para o teorema de Green, ficamos com
Portanto só precisamos descobrir a área da região ! Ela vai ser a área da parábola menos a área da circunferência, vamos fazer cada uma delas separadamente
Passo 3
A área da parábola deve ser feita pela integral dupla mesmo, os limites vão ser esses aqui
Integrando em relação a , fica bem de boinhas
Agora integrando em relação a ficamos com
Essa é a área da parábola, certo? Precisamos retirar aquele círculo desse valor! A área do círculo é definida por
A circunferência é descrita por , portanto o seu raio é igual a , com isso
E a área total pode ser escrita como
Passo 4
Voltando para o resultado que encontramos pelo teorema de Green