Calcule a integral de linha do campo vetorial
ao longo da curva de equação orientada no sentido anti-horário.
Passo 1
Vamos fazer um esboço da curva:
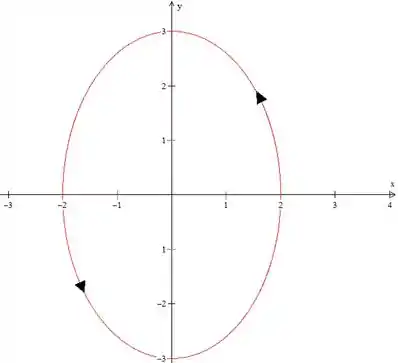
Essa integral de linha parece um pouco complicada de se calcular diretamente pela definição. Vamos, então, usar o Teorema de Green.
Mas aqui temos um problema: o campo não está definido em toda a região dentro da elipse, pois temos uma descontinuidade na origem, se substituirmos na função teremos zero no denominador. O que faremos então? É simples, basta tirarmos a origem da jogada. Se fizermos uma circunferência que “envolva” a origem e chamarmos de a região entre a circunferência e a elipse, o problema está resolvido. Faremos um circunferência de raio para facilitar nossos cálculos. Vamos fazer o novo gráfico para ver como fica essa parada
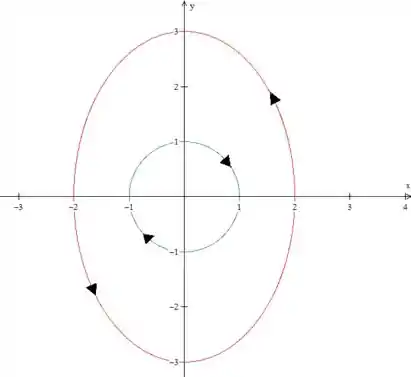
Temos então:
Passando a integral de linha da circunferência pro outro lado (isolando a integral que a gente quer achar) ficamos com
Passo 2
Vamos agora calcular :
Derivando em relação a , vamos precisar usar a regra do quociente que vou te relembrar rapidinho como é
Então fazendo isso pra nossa derivada em relação a ficamos com:
Isso dá pra gente:
Agora para , temos:
Usando de novo a regra do quociente, ficamos com:
Podemos escrever como:
Agora fazendo ficamos com:
Opa! Os termos esquisitos se cancelam, que belezinha, então ficamos com
Passo 3
Aplicando o teorema de Green, temos:
A área de é a área da elipse, dada por (onde e são seus semieixos) menos a do círculo. Então:
Guarde esse resultado. Agora vamos calcular a integral ao longo da circunferência.
Passo 4
Parametrizando a circunferência, temos:
Com variando de a (pois a circunferência está orientada no sentido horário, contrário ao trigonométrico).
Temos
Você poderia utilizar o intervalo de a desde que considerasse que essa integral teria sinal oposto, pois:
Passo 5
Substituindo esses valores na fórmula:
Temos:
Os denominadores vão dar , pela nossa famosa relação , então temos:
Podemos separar eme ficamos com:
Usando a relação de novo, ficamos com:
Passo 6
Agora vamos calcular o valor dessa integral. Para isso usaremos a equação do arco duplo:
Então temos:
Substituindo os valores, temos que:
Passo 7
O que queremos calcular é a integral de linha ao longo de , certo? Substituindo os valores que encontramos em:
Temos, então que: