Calcular a integral de linha da função vetorial
Ao longo da curva que liga o ponto ao ponto e é definida pela equação .
Passo 1
Opaaa, e ai! Vamos continuar no nosso estudo para ficar fera no Teorema de Green!!
Essa integral de linha parece complicada de se calcular diretamente pela definição, não é? O campo vetorial envolve secantes, tangentes, termos não muito agradáveis de se trabalhar! Vamos tentar, então, aplicar o Teorema de Green e ver se encontramos algo mais simples.
A curva em que devemos integrar é uma semicircunferência, pois, elevando a equação ao quadrado, temos
Elevando os dois lados ao quadrado, temos
Passando pro outro lado, temos
Passo 2
Como deve ser maior que zero, queremos a parte de cima da circunferência de raio centrada em . Mas essa curva não é fechada, certo? Então vamos fechá-la na maneira mais simples: com um segmento de reta que liga seus pontos final e inicial.
A curva final será, portanto:
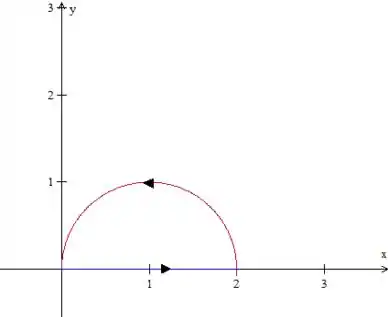
Veja que ela está orientada positivamente, não se esqueça disso!
Aplicando, então, o Teorema de Green, teremos, então:
Então, para achar a integral de linha da nossa curva vamos passar a integral da nossa reta pro outro lado e ficamos com:
Passo 3
Vamos agora calcular :
Aqui o primeiro termo é constante pra gente pois depende só de e estamos derivando em relação a .
Agora :
Por fim:
Passo 4
Aplicando o teorema de Green, temos:
Sendo que
Como se trata de uma semicircunferência de raio , e a área da circunferência é
Assim:
Passo 5
Falta, agora, calcular a integral sobre o segmento , para isso, vamos parametrizá-lo. Como temos o ponto inicial e o final ligados pela reta , uma boa parametrização seria
Onde temos
( é constante e varia).
Derivando essa expressão, temos
Passo 6
Montando a integral de linha sobre teremos:
Então, substituindo nos pontos da nossa função , temos que dá
Veja que escrevemos o campo em função da parametrização de .
Passo 7
Fazendo a diferença entre esses dois resultados, finalmente calculamos a integral sobre :
Como achamos que
Prontinho. Matamos mais essa!