Utilize o Teorema de Green para calcular a integral de linha , onde é a fronteira da região entre e , percorrida no sentido anti-horário.
Passo 1
Vamos esboçar a região para entender melhor o problema. Temos uma reta e uma parábola :
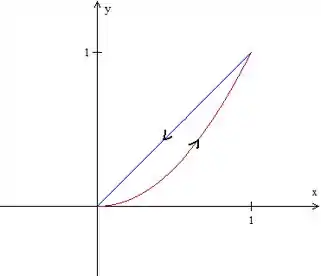
Para podermos aplicar o Teorema de Green, orientamos positivamente a curva.
Passo 2
Vamos relembrar o que diz o teorema de Green? To sentindo que você disse “Siiim” então vambora, o teorema de Green é isso aqui para curvas fechadas, orientada positivamente (sentido anti horário) e sem singularidade
Então vamos calcular
Temos
Então temos que
Ficando com:
Que pode ser escrito desse jeitinho aqui para podermos colocar esse para fora quando formos integrar!
Passo 3
Agora vamos montar a integral dupla, utilizando o Teorema de Green:
Onde é a região limitada pela curva , que vimos lá em cima. Vamos, então, descrever essa região para reescrever essa integral dupla em iterada. Temos que varia entre
Como está na parte de baixo, ela será nosso limite inferior, e está em cima então vai ser nosso limite superior, ok?
E varia entre
(é uma Região do tipo I, lembra dela? Hehe)
Nossa integral passa a ser então:
Passo 4
Começaremos integrando em relação a :
Integrando a parte de dentro:
Passo 5
Agora em relação a resolvendo a integral de fora:
Substituindo os valores, temos
Isso dá
Podemos simplificar os termos e temos
Pra fazer essa soma precisamos encontrar um denominador como a todas das frações. Fazendo o MMC, temos que o denominador é , então ficamos com
Agora que já está com o denominador igual, resolvemos a parte de cima e repetimos a parte de baixo. Que nos dá