Calcule , onde é a parte da curva contida no semiplano orientada no sentido anti-horário.
Passo 1
Faaaala aí! Preparados para mais uma questão de Teorema de Green? Vambora então!
Bom, já deu para ver que calcular essa integral aí pela definição deve dar muito trabalho, né? Vamos tentar aplicar Green então. Temos:
Então vamos calcular
Então temos que
Então, temos que
Bom, como é uma expressão relativamente simples, quer dizer que estamos no caminho certo!
Passo 2
Pelo Teorema de Green, considerando uma curva fechada orientada no sentido anti-horário e a região limitada por ela, temos:
Mas o problema pede a integral de linha na curva contida no semiplano . Ou seja, uma parábola com simetria em , que vai de a :
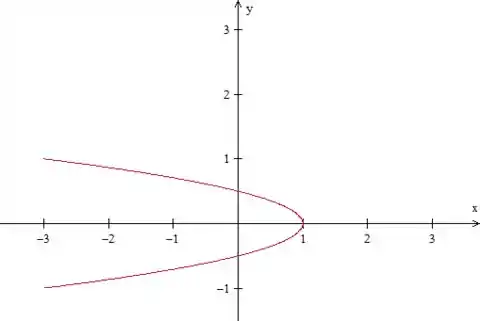
Logo, essa curva é aberta, e para podermos fazer o Teorema de Green é preciso fechá-la!
Então vamos fechá-la, com uma reta mesmo, que liga os pontos final e inicial, no mesmo sentido do arco:
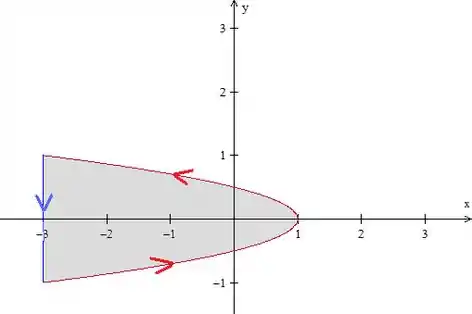
Então, sendo a união a parábola com a o segmento de reta orientados positivamente, temos:
Onde é a região em cinza na figura acima.
Então, para encontrar a integral que queremos, precisamos resolver a integral dupla e a integral de linha na reta.
Passo 3
Vamos começar pela integral dupla. Descrevendo a região como tipo II, temos entre
Como está na esquerda, ele é o nosso limite inferior, e está na direita então ele é nosso limite superior!!
e desde até , como podemos ver na figura.
Levando para a integral, temos:
Passo 4
Então vamos resolver essa integral bonita ai!
Primeiro com a integral de dentro, em relação a
Ajeitando isso, ficamos com essa integral em relação a
Integrando isso ai, ficamos com:
Substituindo os valores temos:
Ajeitando os sinais, temos:
Fazendo o MMC, temos que o denominador vai ser , então ficamos com
Fazendo essas continhas, temos
Passo 5
Agora vamos resolver a integral de linha no segmento de reta. Vamos começar parametrizando o segmento.
Como o segmento pertence à reta , podemos usar essa parametrização aqui:
Onde vai de a (por causa da orientação de ).
Agora vamos derivar essa parametrização:
Escrevendo o campo
Nas variáveis da parametrização, temos:
Que nos dá
Podemos, então, substituir os valores que encontramos na fórmula abaixo:
E isso dá pra gente:
Integral dá trabalho, né? Aqui, você pode pensar no seguinte: como essa função é ímpar (), o seu gráfico é espelhado em relação ao eixo , ou seja, toda a área que temos de a é igual à que temos de a , porém, uma integral terá sinal contrário à outra. Isso quer dizer que a integral de no intervalo de a será igual a zero! Logo, sobra
Passo 6
Ufaaa! achamos, mas calma aí que ainda não acabou! Agora vamos substituir os valores que encontramos para calcular o que o problema pediu:
Que dá
Feinho né? Mas é isso ai haha