Calcule , utilizando o Teorema de Green, onde e é a fronteira da região limitada por e , orientada positivamente.
Passo 1
Oiii, vamos seguir com nossos estudos? Simbora!
Primeiro, vamos fazer um esboço da curva. Como o enunciado fala, temos duas cincunferências, uma de raio e outra de raio .
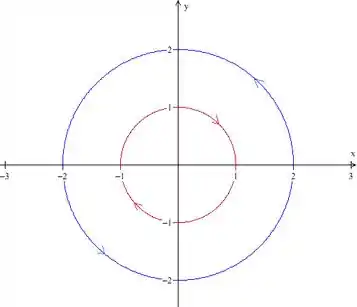
A região limitada pelas curvas é essa coroa, entre o círculo vermelho e o azul.
Cuidado com a orientação da curva, lembre-se do seguinte: para a curva estar orientada positivamente, andando sobre ela, temos que ver a região que ela limita à nossa esquerda. Para a curva de fora, isso significa sentido anti-horário, para a de dentro, sentido horário. Essa é uma condição fundamental para aplicarmos o Teorema de Green!
Passo 2
Beleza, agora precisamos calcular :
Vamos começar com
Derivando em relação a , temos
Agora para
Derivando em relação a temos
Fazendo temos que
Passo 3
Agora podemos montar a integral. Aplicando o teorema de Green, a integral do enunciado pode ser escrita como:
Onde é a região que vimos no passo .
Passo 4
Como a região está compreendida entre duas circunferências, a melhor saída aqui são as coordenadas polares. Faremos:
Pelo próprio gráfico, vemos que , o que equivale a uma volta na circunferência. Os valores de variam entre as duas curvas, logo .
Temos, então:
Não se esqueça desse da mudança para coordenadas polares!
Passo 5
Agora vamos resolver isso aí, integrando em relação a temos:
Resolvendo isso daí, ficamos com
Agora integrando em relação a :