Determine a entropia absoluta em base mássica do gás carbônico que se encontra a e a , usando apenas a tabela entropia absoluta das substâncias a e .
Passo 1
Oi, galera! Esse exercício pede o valor de entropia absoluta em base mássica do que tem uma temperatura de e pressão de ! Isso é a mesma coisa que pedir pra gente o valor da entropia por unidade de massa! O problema é só temos tabelas que informam o valor da entropia por unidade de . Logo, precisamos converter pela fórmula abaixo!
onde é a massa molar da substância. Como a substância é o , a massa molar vale segundo tabelas de gases perfeitos.
No entanto, o exercício só permitiu a gente de usar a tabela abaixo que possui a entropia absoluta das substâncias a e a .
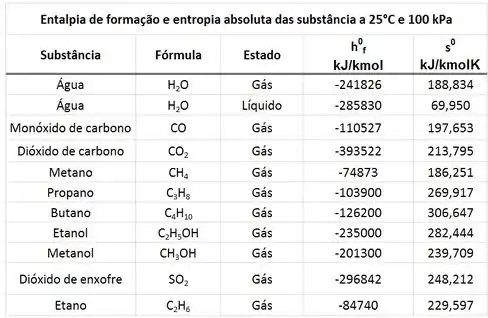
Ou seja, nós precisamos achar o valor da entropia absoluta por do a e , mas nós só podemos usar uma tabela que nos dá o valor da entropia absoluta por do a e . Existe um macetão pra fazer virar . Através da a equação abaixo, achamos a partir de !
onde é a temperatura em kelvin do e é a temperatura de . é o calor específico a pressão constante em .
No próximo passo, veremos como pegar o valor da tabela e como chegar na entropia absoluta .
Passo 2
O valor de se encontra abaixo.
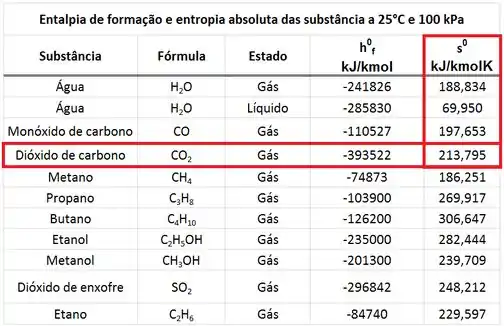
Substituímos a equação de na fórmula de e encontramos:
A divisão de por é o calor específico em encontrado em tabelas de gases perfeitos. Ele vale conforme mostrado abaixo!
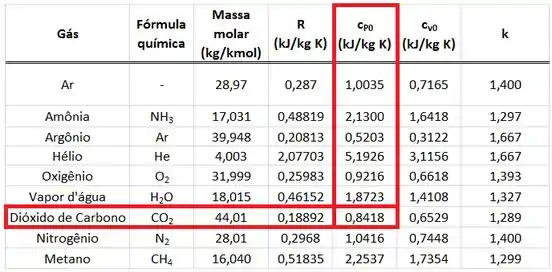
Agora que conseguimos todos esses valores, vamos aprender a usá-los no próximo passo!
Passo 3
Para usar a fórmula, precisamos somar à temperatura em . Substituindo os valores que temos:
Demos uma volta, mas conseguimos achar a entropia absoluta! Paabéns pra gente!