Determine a entropia absoluta em base mássica do gás carbônico que se encontra a e a .
Passo 1
Oi, galera! Esse exercício pede o valor de entropia absoluta em base mássica do que tem uma temperatura de e pressão de ! Isso é a mesma coisa que pedir pra gente o valor da entropia por unidade de massa! O problema é só temos tabelas que informam o valor da entropia por unidade de . Logo, precisamos converter pela fórmula abaixo!
onde é a massa molar da substância. Como a substância é o , a massa molar vale segundo tabelas de gases perfeitos.
Mas temos outro problema! A tabela que temos só serve para gases a de pressão! O exercício quer o valor de entropia pra pressão de ! Por isso, usamos a fórmula abaixo!
onde:
- é a entropia absoluta por a temperatura que queremos e a pressão que queremos;
- é a constante universal dos gases. Seu valor é igual para todos os gases e se encontra abaixo.
- é a entropia absoluta por que está na tabela. Ela é a entropia para a temperatura que queremos, mas para a pressão da tabela;
- é a pressão de tabela em que pegamos o valor da entropia absoluta. No caso, a pressão das tabelas que temos valem .
Como pode ser considerado um gás perfeito, podemos encontrar o valor de entropia absoluta por para temperaturas diferentes de e prassão de em uma tabela. Faremos isso no próximo passo!
Passo 2
Recaptulando, vamos resolver o exercício pegando o valor de entropia absoluta do a e . Depois, vamos usar uma fórmula pra achar a entropia absoluta por do a e . Por fim, convertermos essa entropia pra entropia por unidade de massa através de outra fórmula!

A tabela de pro se encontra abaixo.
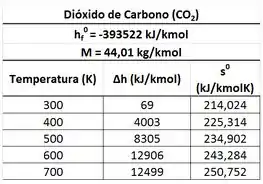
Como podemos, ver a tabela possui valores de entropia para temperaturas em kelvin . Por isso, antes de tudo devemos converter a temperatura em que temos pra , somando ela com .
Agora é só encontar a entropia pra a ! Mas olha que tragédia! Não existe valor de entropia para a temperatura de ! Só existe o valor de entropia pra uma temperatura menor de e outro valor de entropia pra uma temperatura maior de ! O valor que queremos está entre essas duas temperaturas. Logo, vamos interpolar a tabela!
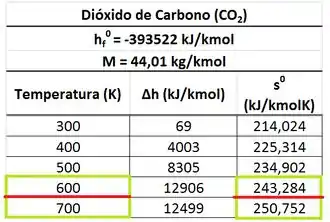
Que show! Achamos o valor interpolado de ! Agora só falta achar e no próximo passo.
Passo 3
Primeiro, convertemos o valor do a e pro valor do a e .
Substituindo esse valor na fórmula da entropia por unidade de massa :
Shoooow de boooola! Mais um exercício pra conta, maninh@!