Determine a entropia absoluta em base mássica do gás metano que se encontra a e a , usando apenas a tabela entropia absoluta das substâncias a e .
Passo 1
Oi, galera! Esse exercício pede o valor de entropia absoluta em base mássica do que tem uma temperatura de e pressão de ! Isso é a mesma coisa que pedir pra gente o valor da entropia por unidade de massa! O problema é só temos tabelas que informam o valor da entropia por unidade de . Logo, precisamos converter pela fórmula abaixo!
onde é a massa molar do que vale segundo tabelas de gases.
No entanto, o exercício só permitiu a gente de usar a tabela abaixo que possui a entropia absoluta das substâncias a e a . Logo, vamos precisar primeiro converter pra entropia do a e a pela fórmula abaixo!
onde é a temperatura em kelvin do e é a temperatura de . é o calor específico a pressão constante em .
Depois, vamos precisar converter pra entropia do a e a pela fórmula abaixo!
é a constante universal dos gases. Seu valor de é igual para todos os gases. é a pressão de na qual o está. é a pressão de tabela em que pegamos o valor da entropia absoluta. No caso, a pressão das tabelas que temos valem .
No próximo passo, veremos como pegar o valor da tabela!
Passo 2
O valor de se encontra abaixo.
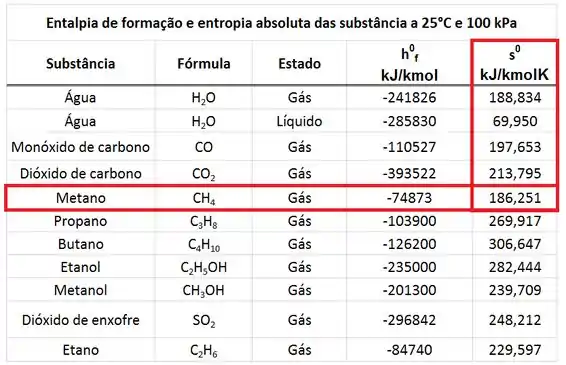
Com esse valor, somos capazes de encontrar o valor da entropia do na temperatura de e na pressão de pela equação abaixo. No entanto, ainda não conhecemos o valor de do . Pra encontrar , precisamos multiplicar o calor específico por unidade de massa do pela massa molar do ! O do vale .
Agora que conseguimos todos esses valores, vamos aprender a usá-los no próximo passo!
Passo 3
Primeiro, vamos encontrar , substituindo os valores de e . Mas cuidado! Antes, de usar a fórmula, precisamos somar à temperatura em .
Em segundo lugar, achamos .
Por fim, encontramos .
Que shooooow! Gostei de ver! Esse exercício foi mais longo, mas resolvemos com muita calma!