Podemos modelar o ar como uma mistura de gases que possui a seguinte análise molar: de e de . Supondo que o ar se encontra a uma pressão total de e a de temperatura, determine a entropia absoluta do ar.
Passo 1
Oi, meus chuchus! Esse exercício quer que a gente calcule a entropia de uma mistura de gases! A entropia da mistura de gases é a soma das entropias de cada gás. No caso, a entropia da mistura é igual à entropia do mais a entropia do . e da fórmula abaixo são as frações molares de e .
No entanto, o está submetido à pressão parcial e o está submetido à pressão parcial . A pressão parcial de é igual à pressão total exercida sobre a mistura multiplicada pela fração molar de . A pressão parcial de é igual à pressão total exercida sobre a mistura multiplicada pela fração molar de .
Isso quer dizer que temos um problema! A tabela que temos só serve para gases a de pressão e o exercício quer o valor de entropia pra pressão parciais diferentes de ! Para resolver esse problemão, convertemos a entropia que encontramos nas tabelas que temos na entropia que está na pressão parcial que queremos, usando as fórmulas abaixo!
é a constante universal dos gases. Seu valor de é igual para todos os gases. é a pressão de tabela em que pegamos o valor da entropia absoluta. No caso, a pressão das tabelas que temos valem .
No próximo passo vamos iniciar as contas!
Passo 2
Primeiro, vamos calcular as pressões parciais e através da pressão total e das frações molares e .
É pra essas pressões parciais que temos que calcular as entropias.
Achamos as entropias do e do nas tabelas de entropia absoluta do e do para a temperatura de . No entanto, pra usar as tabelas, temos que converter pra kelvin, somando !
Uhuuuul! Já temos os valores que precisamos pra achar as entropias nas tabelas!
No próximo passo faremos isso!
Passo 3
se encontra na tabela de abaixo. Como podemos ver, não existe um valer de entropia absoluta para a temperatura exata de . Logo, achamos a entropia absoluta , interpolando a tabela!
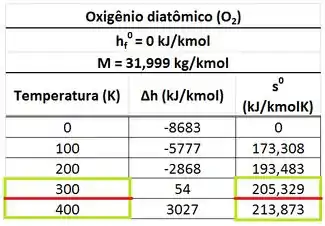
Pelo mesmo motivo, precisamos achar a entropia , interpolando a tabela de entropia absoluta de .
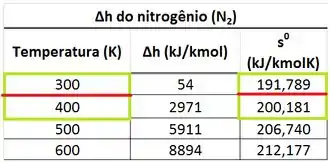
Beleza, essas são as entropias para a pressão total de . Na próxima etapa já vamos conseguir terminar o exercício, determinando as entropias e para as pressões parciais!
Passo 4
Agora, precisamos achar as entropias e pras pressões parciais pelas equações abaixo!
Somando esses dois valores, achamos !
Boaaaaaa! Pode respirar aliviado! Esse é um exercício difícil de entropia absoluta e você conseguiu fazer! Isso quer dizer que você está pronto pra sua prova!