Determine a entropia absoluta em base mássica do gás hidrogênio que se encontra a e a .
Passo 1
Fala, gente! Esse exercício pede o valor de entropia absoluta em base mássica do que tem uma temperatura de e pressão de ! Isso é a mesma coisa que pedir pra gente o valor da entropia por unidade de massa! O problema é só temos tabelas que informam o valor da entropia por unidade de . Logo, precisamos converter pela fórmula abaixo!
onde é a massa molar da substância. Como a substância é o , a massa molar vale:
Esse valor é geralmente encontrado em tabelas de gases perfeitos.
Como pode ser considerado um gás perfeito, podemos encontrar o valor de entropia absoluta por para temperaturas diferentes de em uma tabela parecida com a tabela abaixo.
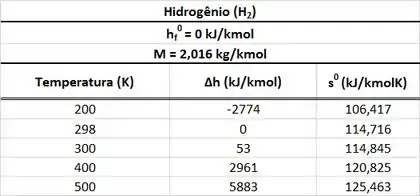
Agora que já conhecemos a tabela de entropia absoluta por unidade de , podemos encontrar o valor que precisamos!
Passo 2
Como podemos, ver a tabela possui valores de entropia para temperaturas em kelvin . Por isso, antes de tudo devemos converter a temperatura em que temos pra , somando ela com .
Agora é só encontar a entropia pra a ! Mas olha que tragédia! Não existe valor de entropia para a temperatura de ! Só existe o valor de entropia pra uma temperatura menor de e outro valor de entropia pra uma temperatura maior de ! O valor que queremos está entre essas duas temperaturas. Logo, vamos interpolar a tabela!
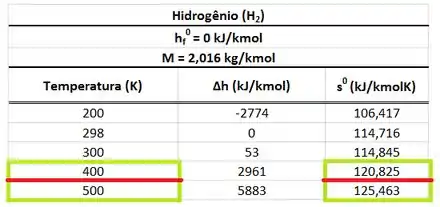
Que show! Achamos o valor interpolado de !
Substituindo esse valor na fórmula da entropia por unidade de massa :
Que iiiiiissso!! Tá ficando craque em cálculo de entropia absoluta, heim?