O conjunto cilindro-pistão mostrado na figura abaixo contém, inicialmente de dióxido de carbono a e . Os pesos são, então, adicionados a uma velocidade tal que o gás é comprimido segundo a relação . Admitindo que a temperatura final seja igual a , determine o trabalho realizado nesse processo.
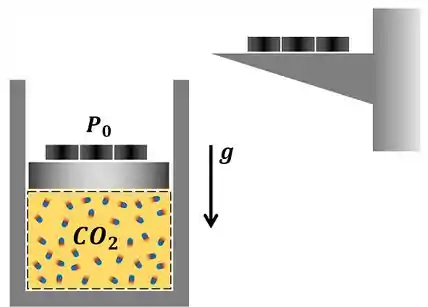
Passo 1
O exercício pede que a gente calcule o trabalho de um processo politrópico de compressão. Mas qual o expoente politrópico do processo? Podemos descobrir isso através da fórmula dada pelo próprio enunciado.
Pela fórmula vemos que o expoente vale 1,2.
A equação de trabalho de um processo politrópico para um expoente diferente de 1 é igual a:
onde o índice 1 aparece nas propriedades do estado 1 do dióxido de carbono e o índice 2 aparece nas propriedades do estado 2 do dióxido de carbono. O estado 1 é o estado inicial. Para ele temos as seguintes infomações.
Para o estado final sabemos apenas que:
Para descobrir a pressão e o volume desse estado, temos que usar a equação de gás perfeito para o estado 2.
Para saber o produto entre pressão e volume do estado 2 só falta encontrar o número de do dióxido de carbono. Como a massa de não varia durante esse processo politrópico, também não varia. Por causa disso, podemos encontrar o do estado 1 e usá-lo na equação do estado 2.
Pronto, temos tudo o que precisamos para calcular o trabalho. Vamos iniciar as contas no próximo passo!
Passo 2
Iniciamos os cálculos pelo valor de .
Agora conseguimos achar o produto entre pressão e volume finais.
Substituindo esse valor na fórmula de trabalho, encontramos:
Conseguimos!!! Achamos o trabalho realizado pelo dióxido de carbono.