de um gás perfeito a contido em um cilindro-pistão expande isobaricamente, provocando uma variação de no seu volume. Considerando que este gás ocupava antes da sua expansão, determine o trabalho realizado pelo gás em joule.

O exercício pede que a gente determine o trabalho de expansão de um gás. O gás faz uma força no êmbolo, colocando o ele em movimento. Esse movimento é possível, porque o gás está dando energia ao pistão através da força que ele produz. Chamamos essa forma de transferência de energia de trabalho.

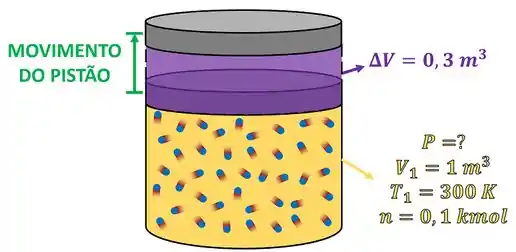
O nome desse tipo de trabalho de mudança de volume do sistema através do movimento de um pistão é chamado de trabalho de movimento da fronteira móvel do sistema. Isso quer dizer que podemos utilizar a seguinte fórmula para calcular o trabalho realizado pelo gás:

onde:

• é a pressão do gás em pascal ;
• é o volume do gás em metro cúbico ;
• é o trabalho realizado pelo gás em joule . Essa é a incógnita do problema.

Mas para usar essa fórmula, precisamos primeiro calcular a pressão inicial do gás. Para isso, usaremos a fórmula de gás perfeito.

sendo:

• ;
• é a constante universal dos gases. Seu valor é igual para todos os gases. Ela vale sempre ;
• é a temperatura do gás antes de expandir. Ela vale segundo o enunciado;
• é o volume que o gás ocupa antes de expandir. Ele vale segundo o enunciado.

Mas como podemos usar essa integral? Por acaso sabemos o valor da pressão em função do volume apara conseguirmos fazer a integração? Sim! Sabemos! Foi dito que o gás se expande isobaricamente. Ou seja, a pressão do gás permanece constante durante o aumento de volume. Logo:

Por isso, a fórmula do trabalho vira:

sendo a variação de volume do sistema durante o processo de expansão. Como o volume do gás aumenta, a variação do volume é positiva. Seu valor é dado pela questão.

Com esse valor, descobrimos que temos todas as informações que precisamos para calcular o trabalho. Então vamos para o próximos passo fazer isso!