Uma organização universitária deseja estimar a porcentagem de estudantes que são favoráveis a criação de um novo estatuto. Ela seleciona uma amostra de 200 estudantes, aleatoriamente, e constata que 120 são favoráveis a este novo estatuto.
(c) Testar a hipótese de ser menor ou igual a 0,55 contra a alternativa de ser maior que 0,55 ao nível de significância de 5%.
Passo 1
Letra c)
Teste de hipóteses! O item dá as hipóteses prontas pra gente:
Hipótese nula com ao invés de ?! Siiim, mas não precisa surtar, a gente vai resolver essa questão como se ali fosse um , não vai fazer diferença na hora dos cálculos.
E como nossa hipótese alternativa é ser maior que alguma coisa, este é um teste unilateral superior!
O nível de significância é 5%, ou seja:
Passo 2
Vamos calcular nossa estatística de teste , que para proporção é dada por:
Temos e .
E vai ser o valor da proporção amostral que estamos testando: 0,55!
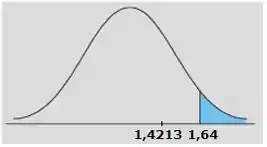
Beleza, agora vamos calcular nossa região crítica. No teste unilateral superior o ponto crítico é dado por:
Então está fora da região crítica! Ou seja, não rejeitamos .
Resposta
Letra c)
Não se rejeita