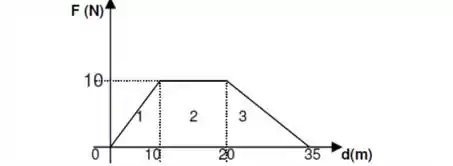
Um corpo de massa movimenta-se em linha reta sobre uma mesa lisa (sem atrito), em posição horizontal, sob a ação de uma força variável que atua na mesma direção do movimento, conforme indica o gráfico abaixo. Calcule o trabalho realizado pela força no deslocamento apresentado
Passo 1
Faaala galerinha! Vamos pra mais uma questão sobre Trabalho!
Bom, na teoria a gente aprende que o trabalho é igual a
“Pô, mas aqui a gente não tem nada, só uma massa e um gráfico, e agora?”
Se liga nessa dica aqui:
Quando temos um gráfico que relaciona a força com a distância, o trabalho vai ser igual a área do gráfico!
Para facilitar, o enunciado já dividiu o gráfico em figuras, vamos achar a área de cada uma delas separadamente e depois vamos somá-las!
Passo 2
Beleza, vamos começar com a área que é um triangulo retângulo! Olhando-o separadamente temos:

Então temos um triangulo retângulo com os dois catetos iguais a . Lembra como calculamos a área de um triângulo?
Em que é a base e é a altura do triângulo. Substituindo os valores, temos
Passo 3
A área é representada assim:
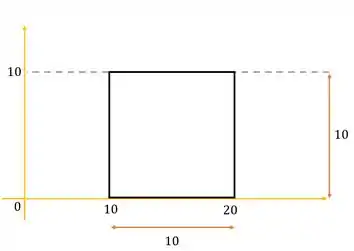
Ou seja, um quadrado de lado
A área de um quadrado é dada por
Em que é o lado do quadrado. Então a área vale
Passo 4
Vamos fazer a mesma coisa para o último triangulo retângulo! Temos que:

Um cateto é igual a e o outro , então a área desse triângulo pode ser calculada por
Ficamos então com:
Agora só precisamos somar as áreas para achar o valor do trabalho