O carro está viajando na velocidade constante de enquanto contorna a curva circular com de raio e no instante representado está na posição . O carro está viajando na velocidade constante de e passa pelo centro do círculo neste mesmo instante. O carro é localizado em relação ao carro pelas coordenadas polares e com o pólo se deslocando com . Para esse instante determine e os valores de e conforme medidos por um observador no carro .
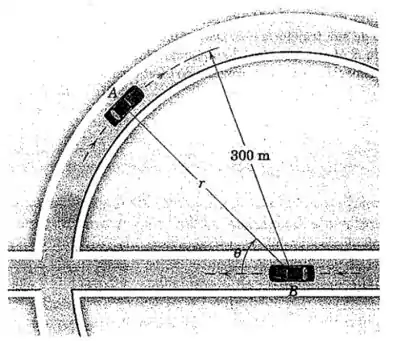
Passo 1
O primeiro passo nesse tipo de questão é localizarmos os vetores velocidade de cada carro:

Podemos juntar os vetores e de modo a construir um triângulo:
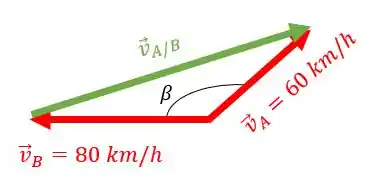
Repare que como queremos o vetor velocidade relativa de com relação a (), então ele deve começar no ponto e chegar até o ponto .
E qual vai ver o ângulo ? É a soma do ângulo que tem entre o vetor e o raio com o ângulo que tem entre o raio e o vetor :
Agora vamos aplicar a lei dos cossenos:
Passo 2
Como o raio é dado em metros, vamos passar as velocidades para e para isso, é só dividir por 3,6:
Nosso próximo passo é calcular as componentes da velocidade na coordenada polar que são as componentes radial e tangencial da velocidade relativa .
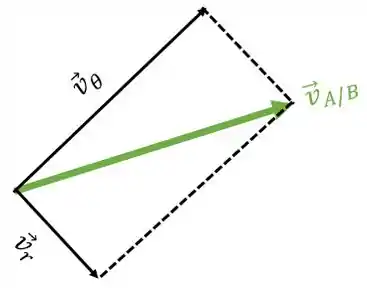
Nas coordenadas polares temos duas componentes para a velocidade:
Vamos ver como fica a coordenada polar na situação inicial do nosso exercício:

Repare que o vetor tem a mesma direção e sentido do vetor , então vamos achar o ângulo entre os vetores e :

Para isso, vamos usar a lei dos senos:
Passo 3
Vamos colocar o ângulo no nosso esqueminha:
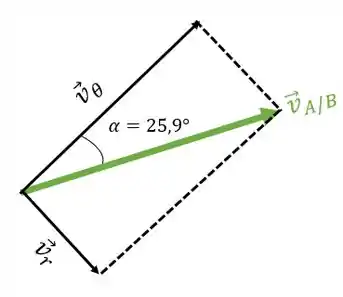
Agora, é decompor o vetor :
Mas lembra que:
Então:
E para ? É só decompor na outra direção:
Temos que:
Então:
O sinal de menos é porque o vetor está no sentido contrário do eixo da coordenada polar:
