Dois aviões, e , voam à mesma altitude. Suas velocidades são e , respectivamente, e seus cursos retilíneos formam um ângulo . Determine a velocidade de em relação à aeronave .
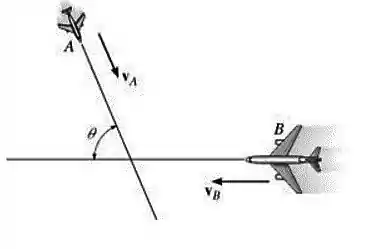
Passo 1
Nosso primeiro passo é localizar os vetores , e . Repare que o vetor velocidade de em relação à aeronave começa no ponto e chega no ponto :
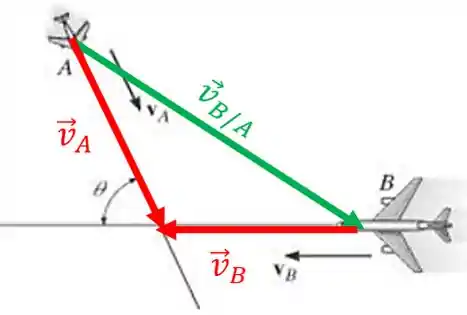
Sabemos que velocidade relativa é:
Então:
Passo 2
Nosso próximo passo é decompor os vetores e no eixo :
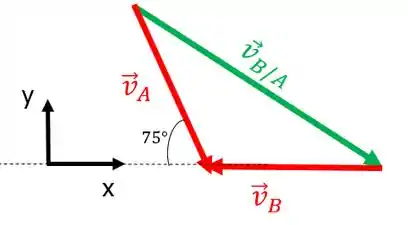
Temos que:
E:
Beleza!
Passo 3
Agora é só somar componente com componente e componente com componente :
Vamos achar o módulo do vetor velocidade relativa de com relação à usando teorema de Pitágoras: