Num dado instante, os carros e trafegam a velocidades de e , respectivamente. Se tem sua velocidade aumentada a uma taxa de , enquanto se mantém com velocidade constante, determine a velocidade e a aceleração de em relação a , nesse instante.
Dados: o raio da curva é ;
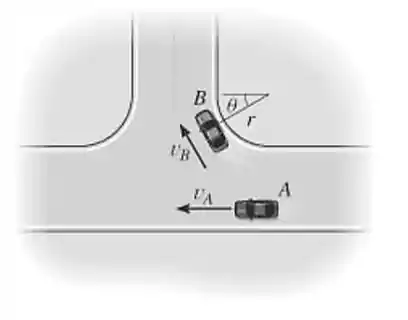
Passo 1
Como ele quer a velocidade de em relação a , o que temos que fazer é nos posicionar em e observar tudo que está fazendo. Vamos ter o seguinte:

Você pode estar se perguntando por que não coloquei o vetor começando em cima do carro . É porque o carro está se movimentando ao longo de uma reta, então posso posicionar o vetor em qualquer ponto ao longo da reta. Beleza?
Sabemos que:
Portanto, podemos escrever:
Passo 2
Para descobrir é só acharmos as componentes de e nos eixos :
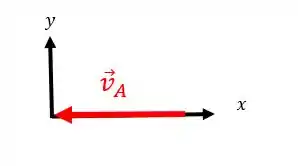
Então:
E ?
Antes de calculá-lo, vamos trabalhar com aquele ângulo dado no enunciado:
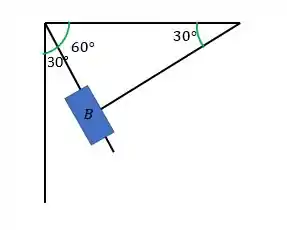
Assim:
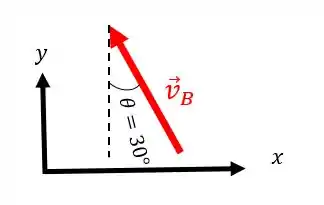
Vamos fazer a soma vetorial agora:
Como a questão pediu o módulo da velocidade relativa, é só aplicarmos o teorema de Pitágoras:
Passo 3
E a aceleração? O carro realiza um movimento retilíneo e sabemos que no movimento retilíneo a aceleração é calculada derivando a velocidade com relação ao tempo:
Como a velocidade do carro é constante, então:
O carro realiza um movimento curvilíneo, então a sua aceleração pode ter duas componentes: uma tangencial e responsável por mudar o módulo da velocidade e uma centrípeta responsável por mudar a direção.
Como no enunciado foi dito que a velocidade do carro aumenta a uma taxa de , já sabemos a componente tangencial da aceleração.
Como a velocidade do carro aumenta, então o vetor tem o mesmo sentido e direção do vetor .
Sabendo que o raio da curvatura é , a aceleração centrípeta vai ser calculada assim:
O vetor sempre aponta para o centro da curva!
Vamos ter o seguinte esquema:
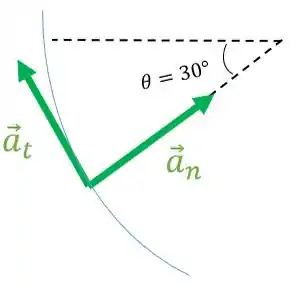
Passo 4
Queremos saber a aceleração de em relação a , não é mesmo? Então:
Vamos isolar o que queremos:
Agora, temos que decompor os vetores aceleração no eixo como fizemos antes com a velocidade.
O vetor terá a mesma decomposição do vetor , já que tem a mesma direção e mesmo sentido do mesmo:
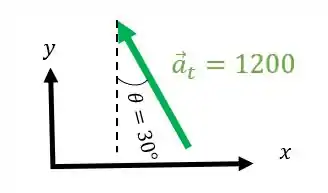
O vetor ficará assim:
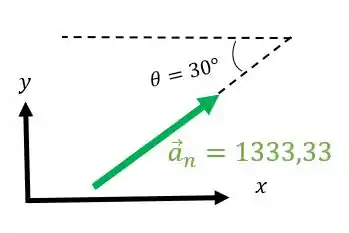
Então, a decomposição será:
O vetor aceleração do carro será:
Passo 5
Calma, já está quase acabando! Vamos substituir as acelerações de cada carro na equação da aceleração relativa:
Então:
Agora, vamos calcular o módulo da aceleração: