O navio está se dirigindo para o oeste a uma velocidade de , e o navio está se dirigindo para o sudeste. A direção relativa de com relação a é de 20° e é invariável. Se a distância entre e é de às , quando a colisão ocorreria se nenhum navio alterasse o curso?
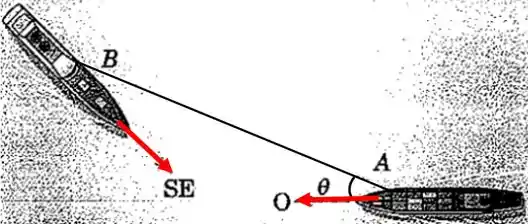
Passo 1
Para começar vamos fazer um esquema com os vetores:
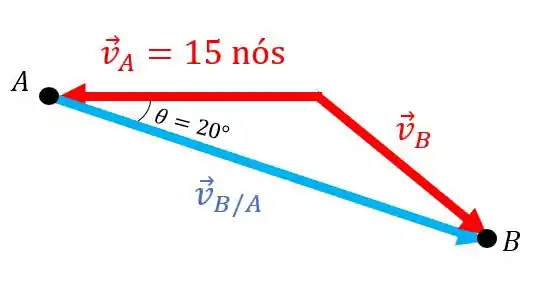
Sabemos que:
Mas não temos os valores da velocidade e nem da velocidade relativa . Então, vamos aplicar a lei dos senos. Para isso, temos que descobrir os ângulos entre os vetores.
Repare que o ângulo entre duas direções da Rosa dos Ventos é de 45°:
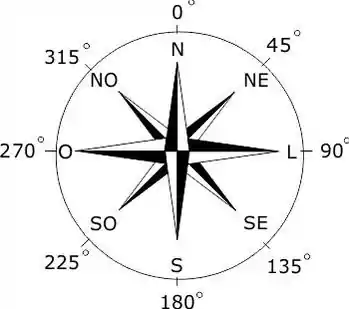
Então, nosso esquema de vetores fica da seguinte forma:
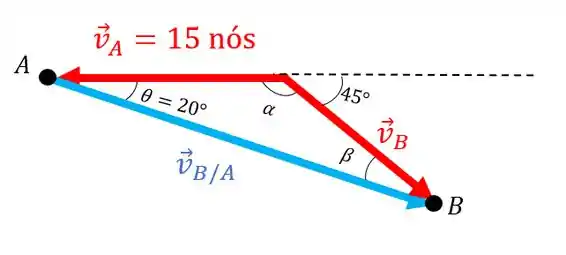
O ângulo entre a direção oeste e a direção sudeste é de 45°. Fica bem mais fácil achar o valor de e de agora:
Passo 2
Beleza! Agora que sabemos os ângulos vamos fazer a lei dos senos:
Uma coisa importante: 1 nó é igual a uma milha marítima por hora!
A questão quer saber o horário da colisão, não é mesmo? Nós temos a distância entre os barcos que é de e temos a velocidade relativa, então:
O tempo inicial é , então temos que acrescentar :
A colisão ocorre às 14h e 24 min!