Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Trocadores de Calor

Ver Teoria
Exercício 12345678

Enunciado

Uma caldeira é alimentada com 5000   k g / h de água líquida a 5   M P a e 20   ° C e descarrega vapor d’água a 450   ° C e 4,5   M P a . Determine as seções de escoamento na alimentação e descarga da caldeira de modo que as velocidades dos escoamentos sejam menores do que 20   m / s .

Passo 1

O exercício pede para a gente calcular a área A e pela qual a água passa para entrar na caldeira e a área A s pela qual a água passa para sair da caldeira. A figura baixo mostra todos os dados fornecidos pelo enunciado para calcular esses valores.

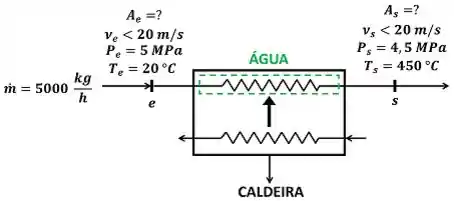
m ˙ é a vazão mássica de água entrando e saindo da caldeira. T e é a temperatura da água entrando na caldeira e T s é a temperatura da água saindo da caldeira. P e é a pressão da água entrando na caldeira e P s é a pressão da água saindo da caldeira. ν e é a velocidade da água entrando na caldeira e ν s é a velocidade da água saindo da caldeira.

Agora que sabemos o que os dados significam, vamos aprender a calcular A e e A s .

Passo 2

Para calcular A e e A s precisamos usar a fórmula da vazão mássica m ˙ abaixo. Ela mostra que a massa especifica ρ multplicada pela velocidade do escoamento ν e pela área de passagem da água A é igual à vazão mássica m ˙ . Essa fórmula serve tanto para a vazão entrando na caldeira quanto para a vazão saindo da caldeira.

m ˙ = ρ e ⋅ A e ⋅ ν e

m ˙ = ρ s ⋅ A s ⋅ ν s

onde ρ e é a massa específica da água entrando na caldeira e ρ s é a massa específica da água saindo da caldeira.

Lembrando que ρ e é o inverso do volume específico da água v e e ρ s é o inverso do volume específico da água v s , conseguimos criar as fórmulas para calcular A e e A s .

m ˙ = ρ e ⋅ A e ⋅ ν e       ⟹       m ˙ = 1 v e ⋅ A e ⋅ ν e       ⟹       A e = m ˙ ⋅ v e ν e

m ˙ = ρ s ⋅ A s ⋅ ν s       ⟹       m ˙ = 1 v s ⋅ A s ⋅ ν s       ⟹       A s = m ˙ ⋅ v s ν s

Calcularemos as duas áreas usando o valor limite das velocidades 20   m / s para saber as áreas de escoamento mínimas.

As fórmulas acima mostram que para calcular A e e A s precisamos dos valores de v e e v s . Encontraremos esses valores no próximo passo.

Passo 3

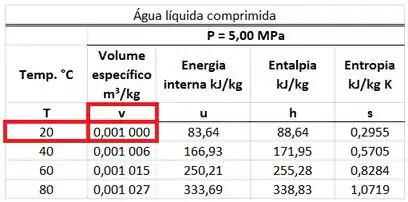
A água que entra na caldeira é um líquido comprimido a 5   M P a e a 20   ° C . Portanto, o valor do volume específico v e desse líquido é encontrado na tabela de líquido comprimido da água. Ele está na mesma linha que a temperatura de 20   ° C e na mesma coluna que v .

v e = 0,001000   m 3 k g

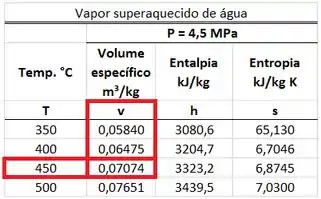
A água que sai da caldeira é um vapor superaquecido a 4,5   M P a e a 450   ° C . Portanto, o valor do volume específico v s desse vapor é encontrado na tabela de vapor superaquecido da água. Ele está na mesma linha que a temperatura de 450   ° C e na mesma coluna que v .

v s = 0,07074 m 3 k g

Com esses dois valores em mãos, nós podemos iniciar as contas!

Passo 4

Antes de usar as fórmulas, nós precisamos converter a vazão mássica m ˙ de k g / h para k g / s .

m ˙ = 5000   k g h       ⟹       m ˙ = 5000 3600   k g s       ⟹       m ˙ = 1,389   k g s

A e = m ˙ ⋅ v e ν e       ⟹       A e = 1,389 ⋅ 0,001000 20       ⟹       A e = 0,00006945   m 2

A s = m ˙ ⋅ v s ν s       ⟹       A s = 1,389 ⋅ 0,07074 20       ⟹       A s = 0,004913   m 2

Resposta

A e = 0,00006945   m 2

A s = 0,004913   m 2

Exercícios de Livros Relacionados

Um trocador de calor adiabático é usado para aquecer água fria a 15 °C, a qual entra no trocador a uma taxa de 5 kg/s por meio de água quente a 90 °C, que por sua vez entra no trocador a uma taxa de 4
17- Um trocador de calor é utilizado para resfriar 3k g / s de ar com água. O ar entra no trocador a 600K e é descarregado a 100° C . A água disponível para alimentar o trocador de calor está a 100k P
16- Os sentidos dos escoamentos num trocador de calor duplo tubo são iguais ( o equipamento opera de modo co-corrente). O tubo interno é alimentado com 1k g / s de ar a 500K e o externo com 2k g / s d
14- Água evapora no interior do tubo de uma caldeira que opera a 100k P a . A velocidade do escoamento de líquido saturado que alimenta o tubo é 1m / s e o tubo descarrega vapor saturado a 100k P a .Q
A pressão e a temperatura da água que escoano ramal de distribuição do edifício mostrado na Fig. P6.74 são iguais a 600k P ae10° C . O ramal está localizado num plano localizado a 5m do chão e a press