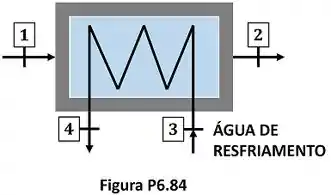
A Fig. P6.84 mostra o esboço de um condensador não misturado (trocador de calor) que é alimentado com de água a e e descarrega líquido saturado a . O fluido de resfriamento é água obtida num lago a e que retorna, ao mesmo tempo, a . Sabendo que a superfície externa do condensador é isolada, calcule a vazão da água de resfriamento.
Passo 1
O enunciado quer saber qual vale a vazão mássica de água do lago ( e ) que é usada para resfriar uma outra corrente de água. A figura abaixo mostra todos os dados que o enunciado nos informa para calcular essa vazão.
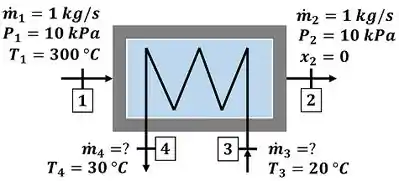
e são a vazão de água quente que passa pelo trocador de calor. As duas têm o mesmo valor porque o escoamento acontece em regime permanente, segundo a fórmula abaixo.
e são a vazão de água de resfriamento do lago que passa pelo trocador de calor. As duas também têm o mesmo valor porque o escoamento acontece em regime permanente, segundo a fórmula abaixo.
é a temperatura da água quente entrando no trocador de calor. é a temperatura da água de resfriamento entrando no trocador de calor. é a temperatura da água de resfriamento saindo do trocador de calor. é a pressão da água quente entrando no trocador de calor. é a temperatura da água quente saindo do trocador de calor. é o titulo da água quente saindo do trocador de calor. Ele vale , porque a água sai do trocador como líquido saturado.

Agora que sabemos o que cada dado significa, vamos aprender a calcular .
Passo 2
pode ser calculado através da equação de primeira lei para um trocador de calor incluindo duas correntes: uma de água quente e outra de água de resfriamento. ATENÇÃO! A forma dessa equação não possui o termo de taxa de troca de calor!
onde é a entalpia específica da água quente entrando no trocador de calor. é a entalpia específica da água quente saindo do trocador de calor. é a entalpia específica da água de resfriamento entrando no trocador de calor. é a entalpia específica da água de resfriamento saindo do trocador de calor.

A fórmula de cima mostra que para calcular precisamos encontrar , , e . Vamos encontar as entalpia e da água quente no próximo passo.
Passo 3
A vazão de água quente é um vapor superaquecido a e a . Logo, para encontar a entalpia , temos que usar a tabela de vapor superaquecido da água. Esse valor está na mesma linha da temperatura de e na mesma coluna da entalpia .
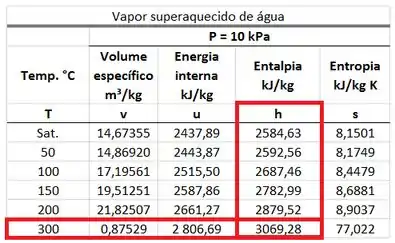
A vazão de água quente é um vapor saturado a . Logo, para encontar a entalpia , temos que usar a tabela de saturação da água. Esse valor está na mesma linha da pressão de e na mesma coluna da entalpia específica do líquido saturado .
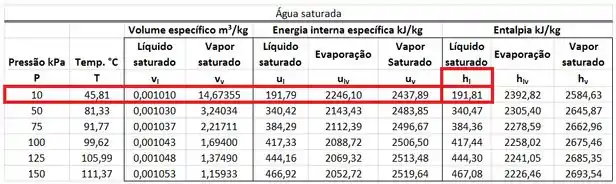
Antes da gente aprender a encontrar as entalpias e da água de resfriamento, temos que aprender a encontrar as pressões e da água de resfriamento. é a pressão da água do lago entrando no trocador e é a pressão da água do lago saindo do trocador. Nós vamos aprender a descobrir esses dois valores na próxima etapa!
Passo 4
A vazão de água de resfriamento vem do lago. Como o lago está a pressão atmosférica de aproximadamente , a vazão também está a .
A vazão de água de resfriamento é despejado de volta no lago. Ou seja, essa vazão também está em contato com o lago que está a pressão atmosférica. Por causa disso, também podemos considerar que a vazão está a pressão atmosférica.
Conhecendo esses dois valores, podemos seguir para a etapa de encontrar e .
Passo 5
As vazões e estão a e têm temperaturas menores que a temperatura de saturação da água a . Isso significa que as vazões e são líquidos comprimidos. No entanto, como não existe tabela de líquido comprimido para , consideraremos como a entalpia do líquido saturado a e como a entalpia do líquido saturado a . Encontramos esses valores na tabela de saturação da água.
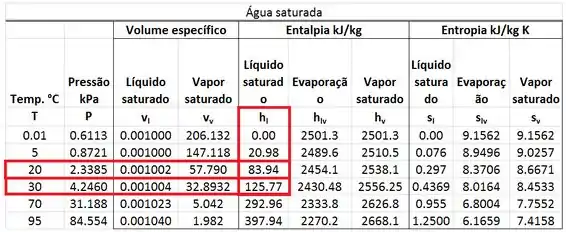
Sabendo todas essas informações, podemos iniciar as contas!