Uma caldeira, que opera em regime permanente, é alimentada com de nitrogênio líquido a . A caldeira descarrega o nitrogênio como vapor saturado a e alimenta um superaquecedor. Sabendo que todos os processos ocorrem em regime permanente e que o superaquecedor descarrega nitrogênio a e , determine as taxas de transferência de calor na caldeira e no superaquecedor.
Passo 1
O exercício pede para a gente calcular a taxa de toca de calor que o nitrogênio troca dentro da caldeira e também a taxa de calor que o nitrogênio troca dentro do superaquecedor. Ou seja, esse exercício envolve dois trocadores de calor: a caldeira e o superaquecedor. A figura baixo mostra todos os dados fornecidos pelo enunciado para calcular esses valores.
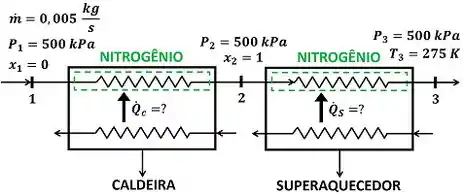
é a vazão mássica de nitrogênio que passa pela caldeira e passa pelo superaquecedor. é a temperatura do nitrogênio saindo do superaquecedor. é a pressão do nitrogênio entrando na caldeira, é a pressão do nitrogênio saindo da caldeira e entrando no superaquecedor e é a pressão do nitrogênio saindo do superaquecedor.

é o título do nitrogênio entrando na caldeira. Ele vale , porque o nitrogênio entra na caldeira como líquido saturado. O enunciado não informa isso, mas quando o nitrogênio está no estado líquido, ele geralmente está saturado. é o título do nitrogênio saindo da caldeira e entrando no superaquecedor. Ele vale , porque o nitrogênio entra na caldeira como vapor saturado.

Agora que sabemos o que os dados significam, vamos aprender a calcular .
Passo 2
é calculado a partir da primeira lei para trocadores de calor em regime permanente aplicada à caldeira. Vale lembrar que, nesse caso, nós estamos estudando apenas uma corrente que passa pela caldeira. Estamos estudando a corrente de nitrogênio. A primeira lei para essa corrente da caldeira é:
é calculado a partir da primeira lei para trocadores de calor em regime permanente aplicada ao superaquecedor. Vale lembrar que, nesse caso, nós estamos estudando apenas uma corrente que passa pelo superaquecedor. Estamos estudando a corrente de nitrogênio. A primeira lei para essa corrente da caldeira é:
Nas fórmulas acima, podemos ver que para calcular e , precisamos encontrar o valor das entalpias específicas do nitrogênio , e . Faremos isso no próximo passo!
Passo 3
A corrente de nitrogênio entrando na caldeira é um líquido saturado a . Logo, o valor da sua entalpia específica é encontrado na tabela de saturação do nitrogênio. Ele é a entalpia específica do líquido saturado a . No entanto, não existe uma linha para a pressão de na tabela de saturação. Por isso teremos que interpolar esse valor!
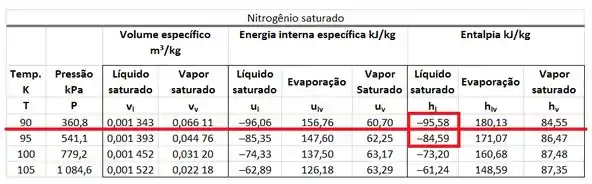
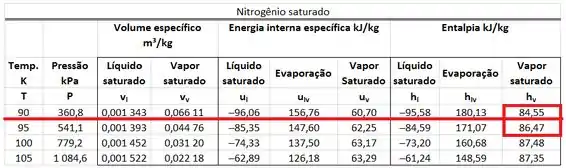
A corrente de nitrogênio saindo da caldeira é um vapor saturado a . Logo, o valor da sua entalpia específica é encontrado na tabela de saturação do nitrogênio. Ele é a entalpia específica do vapor saturado a . No entanto, não existe uma linha para a pressão de na tabela de saturação. Por isso teremos que interpolar esse valor!
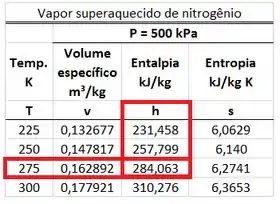
A corrente de nitrogênio saindo do superaquecedor é um vapor superaquecido a . Logo, o valor da sua entalpia específica é encontrado na tabela de nitrogênio superaquecido. Ele está na mesma linha que a temperatura de e na mesma coluna que .
Com esses valores em mãos nós já podemos iniciar as contas!