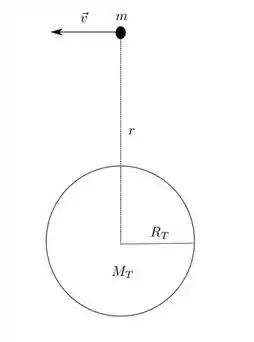
Um objeto com massa m em um dado instante se desloca com velocidade v a uma distância r do centro da terra de forma que r > RT . A velocidade do objeto é perpendicular à linha que liga o objeto ao centro da terra como indicado na figura abaixo. Considere RT o raio da terra, MT a massa da terra e que não há forças dissipativas. Analise se as seguintes afirmações são verdadeiras ou falsas.
( ) Se a interação gravitacional vai fazer com que o objeto mude sua direção de deslocamento e em seguida escape do campo gravitacional da Terra.
( ) Se o objeto orbita a Terra. Considere que ele não colide com a superfície da Terra.
( ) Se o objeto fica orbitando a Terra em uma órbita circular.
( ) Se o objeto não escapa do campo gravitacional da Terra.
Indique a sequência correta de afirmações verdadeiras e falsas.
(a)V,F,V,V
(b) F,V,V,F
(c) F,F,V,F
(d) V,V,F,V
(e) F,V,F,F
(f) F,F,F,V
(g) V,V,F,F
(h) F,F,V,V
(h) F,F,F,F
(h) V,V,V,V
Passo 1
Então, o que tá acontecendo nesse problema? O objeto de massa m tá se deslocando a uma distância r da Terra, com uma velocidade v. Pra esse tipo de situação nós temos duas opções: ou o objeto começa a orbitar a terra, ou ele sai do campo gravitacional da terra.
Pro objeto sair do campo gravitacional da Terra, ele tem que ter uma energia cinética maior que a energia potencial da Terra.
A energia potencial da Terra a gente calcula:
Não liga pra esse sinal de menos! Ele só tá aí pra indicar que em qualquer ponto do campo gravitacional a energia potencial gravitacional é menor do que a do infinito. Na prática nós vamos usar o módulo pra comparar.
E a energia cinética:
Pro objeto parar de orbitar a Terra:
Então se a velocidade for maior ou igual a esse valor aí, o objeto vai sair do campo gravitacional da Terra (não vai orbitar).
Show, então vamos analisar as afirmativas.
Passo 2
( ) Se a interação gravitacional vai fazer com que o objeto mude sua direção de deslocamento e em seguida escape do campo gravitacional da Terra.
Errado! Porque pro objeto sair do campo gravitacional da Terra, v deve ser no mínimo igual a .
( ) Se o objeto orbita a Terra. Considere que ele não colide com a superfície da Terra.
Verdadeiro né? O objeto só escapa do campo gravitacional da Terra se v é maior ou igual a . Então nesse caso, vai orbitar a Terra.
( ) Se o objeto fica orbitando a Terra em uma órbita circular.
Verdadeiro! Mesmo caso da anterior, porque é menor que a velocidade de escape.
( ) Se o objeto não escapa do campo gravitacional da Terra.
Falso! Se v for igual a o objeto já consegue escapar do campo gravitacional da terra.
Ficamos então com:
FVVF
Resposta
Letra B.