Determine o valor da soma vetorial e do ângulo que faz com o eixo positivo . Complete tanto a solução gráfica quanto a algébrica.
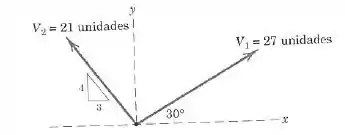
Passo 1
Pra resolver isso de forma algébrica, podemos escrever ambos os vetores em termos de suas componentes.
O vetor fica:
E quanto vale o ângulo que o vetor faz com positivo?
Bom, temos um triângulo semelhante ao triângulo formado pelo vetor e o eixo logo abaixo do mesmo na figura:
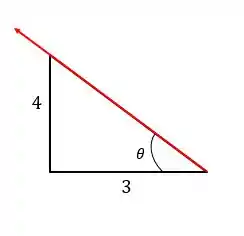
Tirando o arco tangente desse triângulo:
Opa, mas o vetor tá orientado no sentido contrário ao eixo, certo? Então devemos tomar o ângulo suplementar a esse ângulo, ou seja:
Assim:
Passo 2
E pra achar o vetor resultante? Bem, só somar componente a componente:
Passo 3
O vetor resultante faz um ângulo com
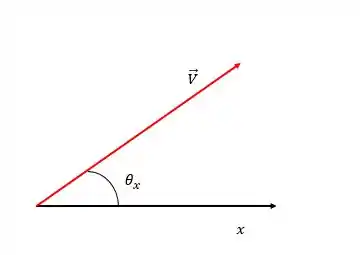
Pra achar esse ângulo, basta a gente tirar o arco tangente das componentes do vetor:
É como se tivéssemos tirado o arco tangente do triângulo formado pelas componentes:
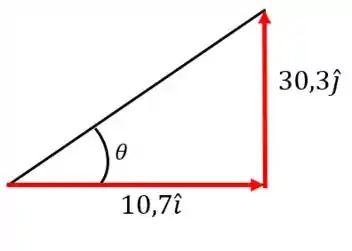
Passo 4
Vamos resolver essa questão agora usando a regra do paralelogramo. Como sabemos os ângulos que cada vetor faz com o eixo , podemos descobrir o ângulo que um vetor faz com o outro, já que a soma de todos os ângulos deve ser igual a
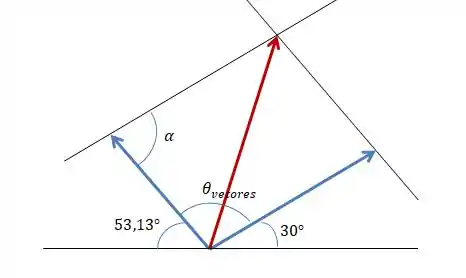
Assim:
Maaaass a gente precisa achar ... e já que num paralelogramo os ângulos opostos são iguais e somando todos dá 360°:
E agora sim vamos aplicar a lei dos cossenos pra achar a resultante: