Para os vetores e abaixo, determine o módulo da diferença vetorial e o ângulo que faz com o eixo positivo Complete tanto a solução gráfica quanto a algébrica.
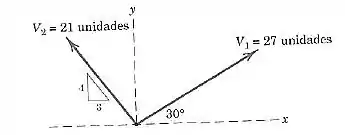
Passo 1
Escrevendo os vetores em termos de suas componentes, temos que:
E para o vetor , temos:
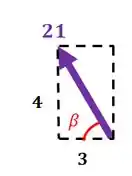
Então:
Pra resolver a questão algebricamente, vamos apenas subtrair componente a componente dos vetores:
Assim:
E:
E pra descobrir o ângulo que o vetor faz com o eixo , basta calcular o usando os valores das componentes:
Mas como queremos o correspondente desse ângulo no 2° quadrante, temos que achar o correspondente dele subtraindo de 180°. Então:
Passo 2
Antes de tudo, lembre-se que uma subtração de vetores é o equivalente a uma soma com um dos vetores com o sentido contrário (com o sinal de menos na frente):
Assim, os nossos vetores vão ficar assim ó:
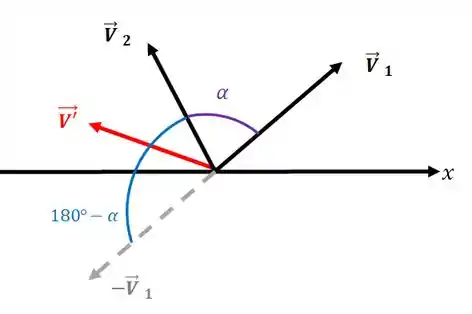
Perceba agora uma coisa: Antes, tínhamos um ângulo entre os vetores. Agora, o ângulo entre os vetores e tem que ser o complementar do antigo ângulo. Repare que o ângulo será:
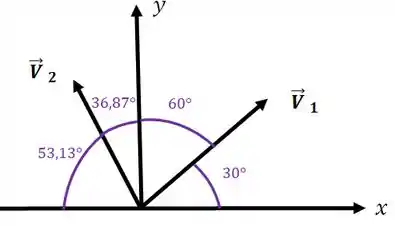
Então:
Assim, basta a gente aplicar a regra do paralelogramo:
Uma diferença pequena para o encontrado no outro método.