Mostrar num gráfico um representante de cada um dos seguintes vetores:
Passo 1
Vamos usar a regra da mão direita pra resolver esse problema.
Mas antes, vamos localizas os nossos vetores unitários lembrando que os vetores e representam os vetores unitários dos eixos e, respectivamente.
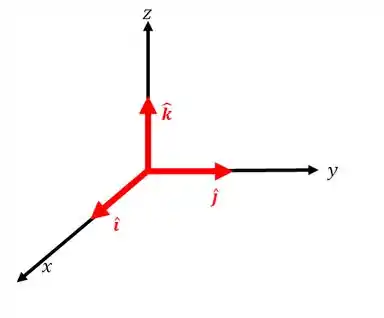
Passo 2
O primeiro produto vetorial é:
Então, vamos achar a direção através da regra da mão direita:
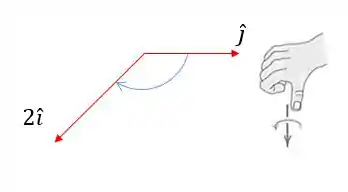
Logo, o vetor resultante é para baixo:
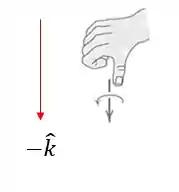
Assim:
E como achamos o módulo? O módulo do vetor vai ser a multiplicação dos módulos! Ou seja:
Ou então, basta lembrar que:
Só que estamos lidando apenas com vetores perpendiculares Assim:
Então, nessa questão, pra achar o módulo é só multiplicar os módulos de cada vetor!
Passo 3
Agora:
Então vamos fazer novamente a regra da mão direita
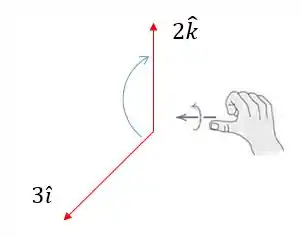
Logo, o sentido do vetor resultante será para a esquerda:
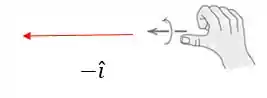
Como o módulo é a multiplicação de cada módulo anterior:
Vamos ter: